Let \(\mathbf{a}=(a_{1},a_{2},\cdots ,a_{n}) \) and \(\mathbf{b}=(b_{1},b_{2},\cdots ,b_{n}) \). Then the dot product of \(\mathbf{a} \) and \(\mathbf{b} \) is the scalar number defined by
$$\mathbf{a}\cdot \mathbf{b}=a_{1}b_{1}+a_{2}b_{2}+ \cdots +a_{n}b_{n}$$
The dot product \(\mathbf{a}\cdot \mathbf{b}\) is a number, unlike the cross product \(\mathbf{a}\times \mathbf{b}\).
Definition is given for n-dimensional vectors. For example, the dot product of 3-dimensional vectors is given as below:
$$\mathbf{a}\cdot \mathbf{b}=(a_{1},a_{2},a_{3}) \cdot (b_{1},b_{2},b_{3})=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$$
Example : $$\begin{eqnarray*}(7, -5)\cdot (3, 0)&=&7\cdot 3+(-5)\cdot 0=21 \\(-1, 3, 5) \cdot (2, -3, \frac{1}{7})&=&(-1)\cdot 2+3\cdot (-3)+5\cdot \frac{1}{7}=-\frac{72}{7}\end{eqnarray*}$$
Properties
Let \(\mathbf{a},\ \mathbf{b} \) and \(\mathbf{c} \) be are vectors, and m be a scalar.
Then, the dot products of vectors have the following properties:
$$\begin{eqnarray*}&&\mathbf{a}\cdot \mathbf{a}=|\mathbf{a}|^{2}\\
&&\mathbf{a}\cdot \mathbf{b}=\mathbf{b}\cdot \mathbf{a}\\
&&\mathbf{a}\cdot (\mathbf{b}+ \mathbf{c})=\mathbf{a}\cdot \mathbf{b}+\mathbf{a}\cdot \mathbf{c}\\
&&(m\mathbf{a})\cdot \mathbf{b}=m(\mathbf{a}\cdot \mathbf{b})=\mathbf{a}\cdot (m\mathbf{b})\\
\end{eqnarray*}$$
Here are the some proofs of Properties :
$$\begin{eqnarray*}&&\mathbf{a}\cdot \mathbf{a}=a_{1}a_{1}+a_{2}a_{2}+ \cdots +a_{n}a_{n}\\&&\ \ \ \ \ \ \ =a_{1}^{2}+a_{2}^{2}+ \cdots +a_{n}^{2}\\&&\ \ \ \ \ \ \ =|\mathbf{a}|^{2}\\&&\ \ \\&&\ \ \\&&\mathbf{a}\cdot (\mathbf{b}+\mathbf{c})=(a_{1},a_{2},a_{3})\cdot (b_{1}+c_{1},b_{2}+c_{2},b_{3}+c_{3})\\&&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =a_{1}(b_{1}+c_{1})+a_{2}(b_{2}+c_{2})+a_{3}(b_{3}+c_{3})\\&&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3})+(a_{1}c_{1}+a_{2}c_{2}+a_{3}c_{3})\\&&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\mathbf{a}\cdot \mathbf{b}+\mathbf{a}\cdot \mathbf{c}\end{eqnarray*}$$
Another properties are also easily proved by using Definition.
Another definition of the dot product
Let \(\theta\) be the angel between \(\mathbf{a}\) and \(\mathbf{b}\). Then
$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}| |\mathbf{b}|\cos\theta$$
This formula is often used as the definition of the dot product by physicists. From the theorem, you can see that
- \(\mathbf{a}\cdot \mathbf{b}>0\), if \(0\leq \theta \) < \(\frac{\pi}{2}\) (since \(\cos \theta>0\) ).
- \(\mathbf{a}\cdot \mathbf{b}=0\), if \(\theta=\frac{\pi}{2}\) (since \(\cos \theta=0\) ).
- \(\mathbf{a}\cdot \mathbf{b}<0\), if \(\frac{\pi}{2}\) < \( \theta <\pi\) (since \(\cos \theta<0\) ).

Specially,
- If \(\theta=0\), \(\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}| |\mathbf{b}|\) . (That is, none zero two vectors \(\mathbf{a}\) and \(\mathbf{b}\) point in exactly the same direction.)
- If \(\theta=\pi\), \(\mathbf{a}\cdot \mathbf{b}=-|\mathbf{a}| |\mathbf{b}|\) . (That is, none zero two vectors \(\mathbf{a}\) and \(\mathbf{b}\) point in exactly opposite direction.)
- If \(\theta=\frac{\pi}{2}\), \(\mathbf{a}\cdot \mathbf{b}=0\) . (That is, none zero two vectors \(\mathbf{a}\) and \(\mathbf{b}\) are orthononal if and only if \(\mathbf{a}\cdot \mathbf{b}=0\).)
Furthermore, by the formula, we can find the angle between two vectors as below:
$$\cos\theta=\frac{\mathbf{a}\cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|}$$
Example : Find the angle between the vectors \(\mathbf{a}=(2, -1), \ \mathbf{b}=(3,1)\).
Solution : Since \(|\mathbf{a}|=\sqrt{2^{2}+(-1)^{2}}=\sqrt{5} \ \ \ \ \text{and} \ \ \ \ \ |\mathbf{b}|=\sqrt{3^{2}+(1)^{2}}=\sqrt{10}\) and since \(\mathbf{a}\cdot \mathbf{b}=2\cdot 3 + (-1)\cdot 1 =5\), we have
$$\cos\theta=\frac{\mathbf{a}\cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|}=\frac{5}{\sqrt{5}\sqrt{10}}=\frac{1}{\sqrt{2}}$$
So the angle between \(\mathbf{a} \) and \(\mathbf{b} \) is \(\theta=\frac{\pi}{4}=45^{\circ}\).
Proof
Let \(\theta\) be the angle between \(\mathbf{a}\) and \(\mathbf{b}\) that start at the origin or the angle between line segments OA and OB as shown in Figure.
Then if we apply the Law of Cosine to triangle OAB, we have
$$|AB|^{2}=|OA|^{2}+|OB|^{2}-2|OA| |OB|\cos \theta\ \ \cdots \ (1)$$
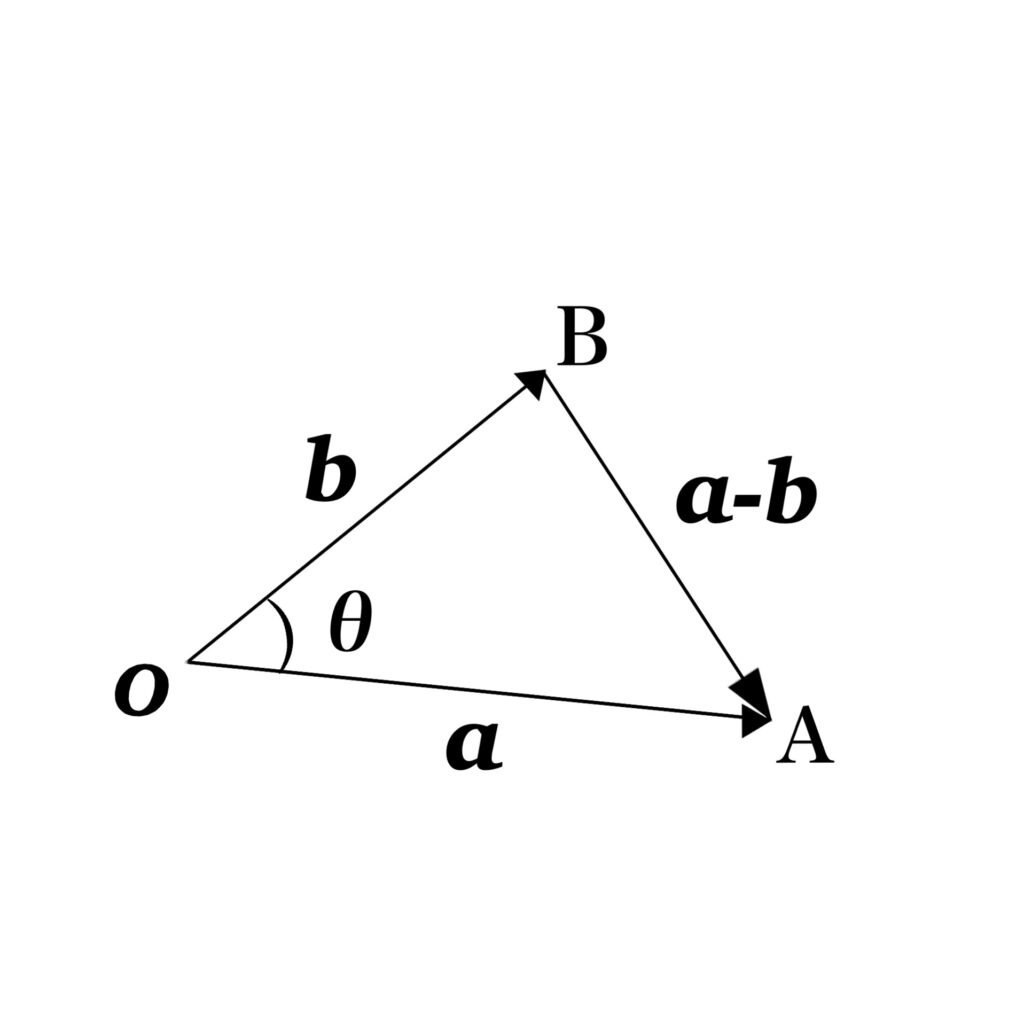
Then applying \(|OA|=|\mathbf{a}|,\ |OB|=|\mathbf{b}|,\ |AB|=|\mathbf{a}-\mathbf{b}|\), the above equation becomes
$$|\mathbf{a}-\mathbf{b}|^{2}=|\mathbf{a}|^{2}+|\mathbf{b}|^{2}-2|\mathbf{a}| |\mathbf{b}|\cos \theta\ \ \cdots \ (2)$$
Using the properties of the dot product, we can rewrite the LHS of (2) as follows:
$$\begin{eqnarray*}|\mathbf{a}-\mathbf{b}|^{2}&=&(\mathbf{a}-\mathbf{b})\cdot (\mathbf{a}-\mathbf{b})\\&=&\mathbf{a}\cdot \mathbf{a}-\mathbf{a}\cdot \mathbf{b}-\mathbf{b}\cdot \mathbf{a}+\mathbf{b}\cdot \mathbf{b}\\&=&|\mathbf{a}|^{2}-2\mathbf{a}\cdot \mathbf{b}+|\mathbf{b}|^{2}\end{eqnarray*}$$
Therefore, we have
$$|\mathbf{a}|^{2}-2\mathbf{a}\cdot \mathbf{b}+|\mathbf{b}|^{2}=|\mathbf{a}|^{2}+|\mathbf{b}|^{2}-2|\mathbf{a}| |\mathbf{b}|\cos \theta$$
Thus, we get
$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}| |\mathbf{b}|\cos\theta$$