$f(x)=\tan x$($-\frac{\pi}{2}\leq x\leq \frac{\pi}{2}$) の逆関数を $f^{-1}(x)=\tan^{-1} x$ (または $\mathrm{arctan}\ x$ ) で表し, 逆正接(アークタンジェント)という. すなわち
$$y=\tan^{-1} x \Longleftrightarrow x=\tan y$$
ただし $y=\tan^{-1} x$ の定義域は $-1\leq x\leq 1$, 値域は $-\infty\leq y \leq\infty$ となる.
$y=\tan x$ は単調関数(1:1対応)でないため, 逆関数が定義できない.
ただし定義域を $-\frac{\pi}{2} \leq x \leq\frac{\pi}{2}$ に制限すれば, $y=\tan x$ は単調増加関数となり逆関数が存在する.

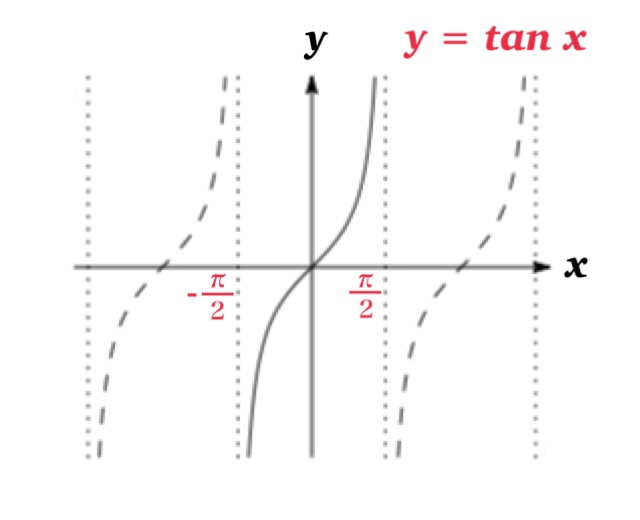
このとき, $f(x)=\tan x$ の定義域は$-\frac{\pi}{2}\leq x\leq \frac{\pi}{2}$, 値域は $-\infty\leq y \leq \infty$ より, 逆関数 $f^{-1}(x)=\tan^{-1} x$ の定義域は $-\infty\leq x \leq \infty$, 値域は$-\frac{\pi}{2}\leq y\leq \frac{\pi}{2}$ となる.
注意:グラフより $\tan^{-1}(-x)=-\tan^{-1} x$ であることがわかる.

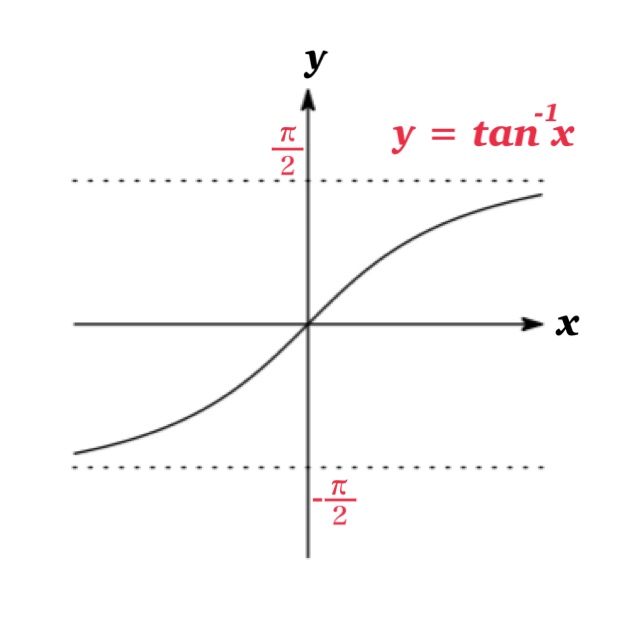
例:次の値を求めよ.
$$\tan^{-1}\sqrt{3},\ \ \ \tan^{-1}(\frac{\sqrt{3}}{3}),\ \ \ \cos^{-1}(-\sqrt{3})$$
解答
$\tan(\frac{\pi}{3})=\sqrt{3}, \ \tan(\frac{\pi}{6})=\frac{\sqrt{3}}{3}, \ \tan(-\frac{\pi}{3})=-\sqrt{3}$ より
$$\tan^{-1}\sqrt{3}=\frac{\pi}{3},\ \ \tan^{-1}(\frac{\sqrt{3}}{3})=\frac{\pi}{6},\ \ \ \text{and}\ \ \ \tan^{-1}(-\sqrt{3})=-\frac{\pi}{3}$$
導関数
\begin{eqnarray*}&&\frac{d}{dx} (\tan^{-1} x)=\frac{1}{1+x^{2}}\\
&&\frac{d}{dx} (\tan^{-1} f(x))=\frac{f'(x)}{1+f(x)^{2}}\end{eqnarray*}
$y=\tan^{-1} x$ とするとき, $x=\tan y$ と表すことができる. (ただし $-\frac{\pi}{2}\leq y\leq\frac{\pi}{2}$)
逆関数の微分法により $y=\tan^{-1} x$ を微分すれば
$$\begin{eqnarray*}\frac{d}{dx}(\tan^{-1} x)&=&\frac{dy}{dx}=\frac{1}{\ \ \frac{dx}{dy}\ \ }\\&=&\frac{1}{\frac{d}{dy}(\tan y)}=\frac{1}{\ \frac{1}{\cos^{2}y}\ }\\&=&\frac{1}{1+\tan^{2} y}=\frac{1}{1+x^{2}}\end{eqnarray*}$$
よって
$$\frac{d}{dx} (\tan^{-1} x)=\frac{1}{1+x^{2}}$$
また合成関数の微分法を用いれば次を得る:
$$\frac{d}{dx} (\tan^{-1} f(x))=\frac{f'(x)}{1+f(x)^{2}}$$
例
$f(x)=\tan^{-1}3x^{2}$ とするとき, $f'(x)$ を求めよ.
解答 $f'(x)=\frac{1}{1+(3x^{2})^{2}}\frac{d}{dx}(3x^{2})=\frac{6x}{1+9x^{4}}$.
不定積分
微分公式より以下を得る:
\begin{eqnarray*}&&(1)\ \ \ \int \frac{1}{1+x^{2}}\ dx=\tan^{-1}x +C \\
&&(2)\ \ \ \int \frac{1}{a^{2}+(px+q)^{2}}\ dx=\frac{1}{ap}\tan^{-1}\frac{px+q}{a} +C\end{eqnarray*}
(1) $\frac{d}{dx} (\tan^{-1} x)=\frac{1}{1+x^{2}}$ より $\int \frac{1}{1+x^{2}}\ dx=\tan^{-1}x +C$ は明らか.
(2) $\int \frac{1}{\sqrt{a^{2}+(px+q)^{2}}}\ dx$ を求めるために, 次のように書き替える:
\begin{eqnarray*}\int \frac{1}{a^{2}+(px+q)^{2}}\ dx&=&\int \frac{(\frac{px+q}{a})’\cdot \frac{a}{p}}{a^{2}\{1+(\frac{px+q}{a})^{2}\}}\ dx\\&=&\int \frac{1}{ap}\cdot \frac{(\frac{px+q}{a})’}{1+(\frac{px+q}{a})^{2}}\ dx\\&=&\frac{1}{ap}\tan^{-1}(\frac{px+q}{a})+C\end{eqnarray*}
または $t=\frac{px+q}{a}$ として置換積分を行えば
$\frac{dt}{dx}=\frac{p}{a}$, $dt=\frac{p}{a}dx$ より
\begin{eqnarray*}\int \frac{1}{a^{2}+(px+q)^{2}}\ dx&=&\frac{1}{ap}\int \frac{1}{1+(\frac{px+q}{a})^{2}}\ \frac{p}{a}dx\\&=&\frac{1}{ap}\int \frac{1}{1+t^{2}}\ dt\\&=&\frac{1}{ap}\tan^{-1} t +C\\&=&\frac{1}{ap}\tan^{-1}(\frac{px+q}{a})+C\end{eqnarray*}
例
$\int \frac{x}{x^{4}+x^{2}+1}\ dx$ を求めよ.
解答 積分公式を用いるために, $\frac{x}{x^{4}+x^{2}+1}$ を次のように書き替える:
\begin{eqnarray*}\frac{x}{x^{4}+x^{2}+1}&=&\frac{x}{(x^{4}+2x^{2}+1)-x^{2}}\\&=&\frac{x}{(x^{2}+1)^{2}-x^{2}}\\&=&\frac{x}{(x^{2}-x+1)(x^{2}+x+1)}\\&=&\frac{1}{2}\left(\frac{1}{x^{2}-x+1}-\frac{1}{x^{2}+x+1}\right)\end{eqnarray*}
よって
\begin{eqnarray*}\int \frac{x}{x^{4}+x^{2}+1}\ dx&=&\int \frac{1}{2}\left(\frac{1}{x^{2}-x+1}-\frac{1}{x^{2}+x+1}\right)\ dx\\&=&\frac{1}{2}\left( \int \frac{1}{(x-\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}\ dx -\int \frac{1}{(x+\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}\ dx\right)\\&=&\frac{1}{\sqrt{3}} \left(\tan^{-1}\frac{2x-1}{\sqrt{3}}-\tan^{-1}\frac{2x+1}{\sqrt{3}} \right)+C\end{eqnarray*}