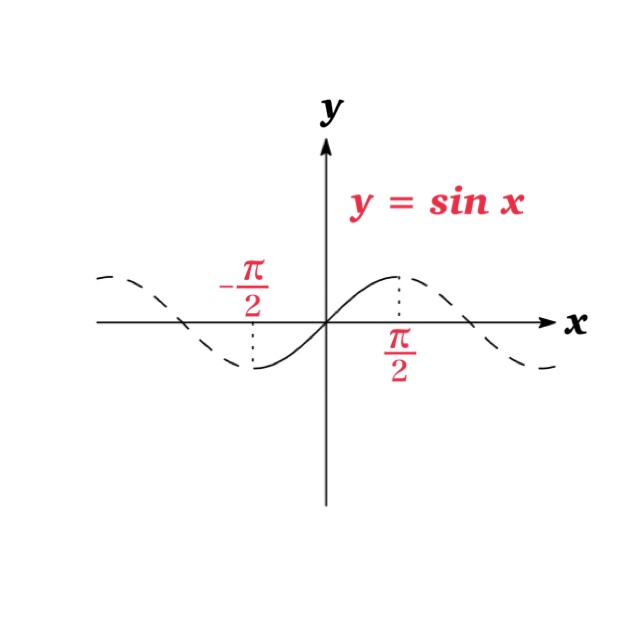
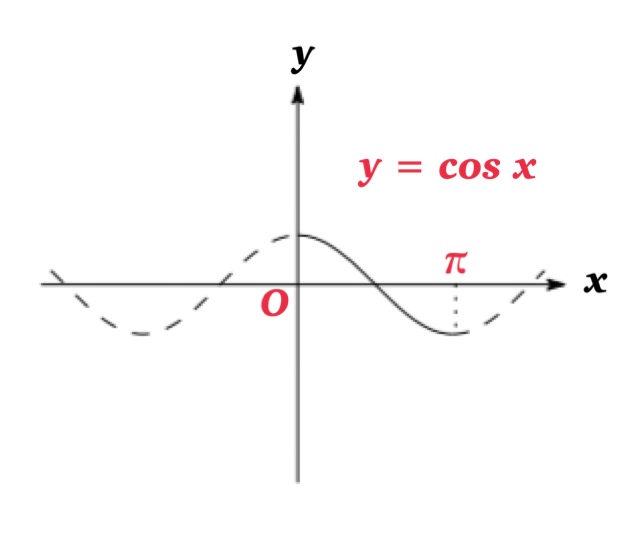
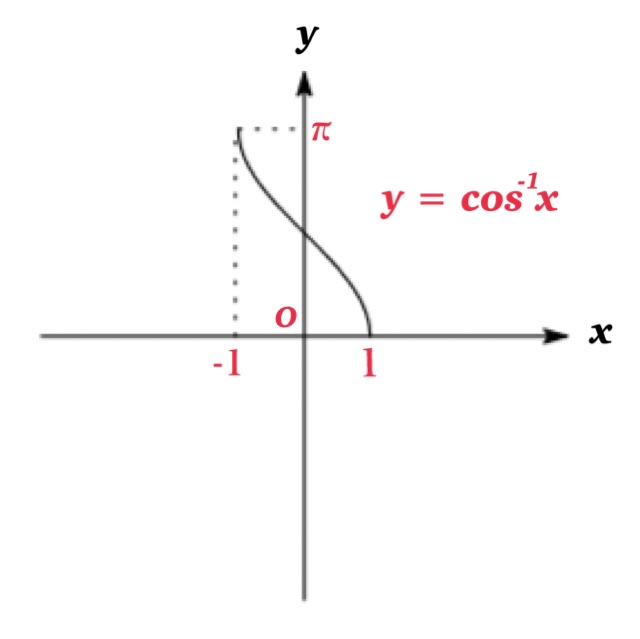
関数 $y=\sin x,\ \cos x,\ \tan x$ の逆関数は次で定義される: \begin{eqnarray*}y=\sin^{-1} x &\Longleftrightarrow & \sin y=x\ \ \ \ \ (-\frac{\pi}{2}\leq y\leq \frac{\pi}{2})\\\ y=cos^{-1} x &\Longleftrightarrow & \cos y=x\ \ \ \ \ ( 0 \leq y \leq \pi ) \\\ y=tan^{-1} x &\Longleftrightarrow & \tan y=x\ \ \ \ \ (-\frac{\pi}{2} < y < \frac{\pi}{2})\end{eqnarray*} ただし三角関数は単調関数でないため, 定義域を制限することで逆関数が定義される.
三角関数 $y=\sin x,\ \cos x,\ \tan x$ はそれぞれ単調関数 (1:1 対応)でないため, 逆関数が定義できない.
ただし定義域を制限することにより, 単調関数となり逆関数が定義できる.
注意: $\sin^{-1}(x)\not= \frac{1}{\sin x}$ である. 他も同様.
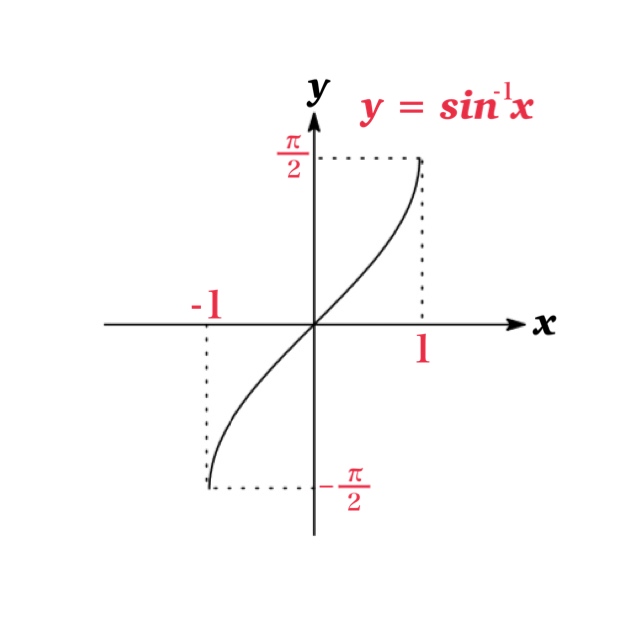
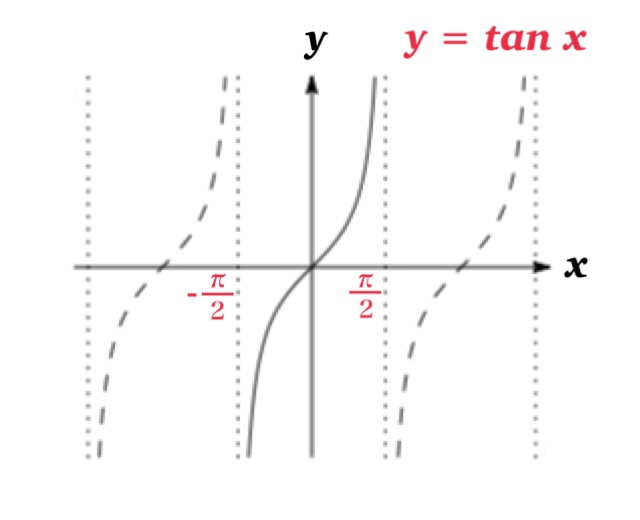
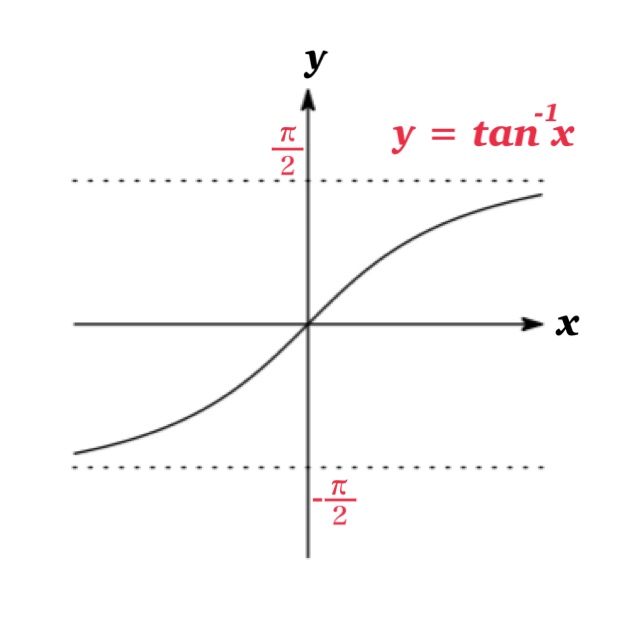
| 逆三角関数 | 定義域 | 値域 |
| 逆正弦(アークサイン) \(y=\sin^{-1} x\) | \(-1\leq x\leq 1\) | \(-\frac{\pi}{2}\leq y\leq \frac{\pi}{2}\) |
| 逆余弦(アークコサイン) \(y=\cos^{-1} x\) | \(-1\leq x\leq 1\) | \(0\leq y\leq \pi\) |
| 逆正弦(アークタンジェント) \(y=\tan^{-1} x\) | \(-\infty \)<\( x< \infty\) | \(-\frac{\pi}{2}\) < \( y\) < \(\frac{\pi}{2}\) |
対称性
| $\sin^{-1}(-x)=-\sin^{-1}x$ |
| $\tan^{-1}(-x)=-\tan^{-1}x$ |
Notice:$\cos^{-1}(-x)\not=-\sin^{-1}x$
導関数
| $\frac{d}{dx} (\sin^{-1} x)=\frac{1}{\sqrt{1-x^{2}}}$ |
| $\frac{d}{dx} (\cos^{-1} x)=-\frac{1}{\sqrt{1-x^{2}}}$ |
| $\frac{d}{dx} (\tan^{-1} x)=\frac{1}{1+x^{2}}$ |
| $\frac{d}{dx} (\sin^{-1} f(x))=\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}$ |
| $\frac{d}{dx} (\cos^{-1} f(x))=-\frac{f'(x)}{\sqrt{1-{f(x)}^{2}}}$ |
| $\frac{d}{dx} (\tan^{-1} f(x))=\frac{f'(x)}{1+f(x)^{2}}$ |
不定積分
| $\int \frac{1}{\sqrt{1-x^{2}}}\ dx=\sin^{-1}x +C$ |
| $\int \frac{1}{\sqrt{1-x^{2}}}\ dx=-\cos^{-1}x +C$ |
| $\int \frac{1}{1+x^{2}}\ dx=\tan^{-1}x +C$ |
| $\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx=\frac{1}{p}\sin^{-1}\frac{px+q}{a} +C$ |
| $\int \frac{1}{\sqrt{a^{2}-(px+q)^{2}}}\ dx=-\frac{1}{p}\cos^{-1}\frac{px+q}{a} +C$ |
| $\int \frac{1}{a^{2}+(px+q)^{2}}\ dx=\frac{1}{ap}\tan^{-1}\frac{px+q}{a} +C$ |