$a$ を正の定数とするとき
$$f(x)=a^{x}$$
で表される関数を $a$ を底とする指数関数という. (一般に $a\not= 1$ とする.)
特に底を $e$ (ネイピア数)とする指数関数 $f(x)=e^{x}$ は自然指数関数と呼ばれ, 微分や積分との相性が良い.
一般に「指数関数」は自然指数関数 $f(x)=e^{x}$ を指す場合が多い.
指数法則
| \(x\) | \(y=a^{x}\) | Example |
| \(x=0\) | \(a^{0}=1\) | \(3^{0}=1\) |
| $n$ が正整数のとき | \(a^{n}=\overbrace{a\cdot a\cdots a}^{n\ \text{factors}} \) | \(2^{3}=2\cdot 2\cdot 2=8\) |
| $r$ が実数のとき | \(a^{-r}=\frac{1}{a^{r}}\) | \(2^{-3}=\frac{1}{2^{3}}=\frac{1}{8}\) |
| $p, q$ が整数のとき ただし\(p>0\) | \(a^{\frac{q}{p}}=\sqrt[p]{a^{q}}=(\sqrt[p]{a})^{q}\) | \(2^{\frac{5}{3}}=\sqrt[3]{2^{5}}=(\sqrt[3]{2})^{5}\) |
指数法則
$a\not= 0$, $b\not=0$, $n$ と $m$ を整数とする.
| 指数法則 | Example |
| \(a^{n+m}=a^{n}a^{m}\) | \(a^{2}a^{3}=(a\cdot a)\cdot (a\cdot a\cdot a)=a^{2+3}=a^{5}\) |
| \(a^{n-m}=\frac{a^{n}}{a^{m}}\) | \(\frac{a^{5}}{a^{3}}=\frac{a\cdot a\cdot a\cdot a\cdot a}{a\cdot a\cdot a}=a^{5-3}=a^{2}\) |
| \(\left(a^{n}\right)^{m}=a^{nm}\) | \(\left(a^{2}\right)^{3}=a^{2}\cdot a^{2}\cdot a^{2}=a^{2\times 3}=a^{6}\) |
| \((ab)^{n}=a^{n}b^{n}\) | \((ab)^{3}=(ab)\cdot (ab)\cdot (ab)=a^{3}b^{3}\) |
グラフ
| Fig. 1 | \(0<a<1\)のとき \(y=a^{x}\) は単調減少. |
| Fig. 2 | \(a=1\)のとき \(y=1^{x}\) 定数. |
| Fig. 3 | \(1<a\)のとき \(y=a^{x}\) は単調増加. |
| Fig. 4 | Notice: \(y=\left(\frac{1}{a}\right)^{x}\) のグラフ は $(\frac{1}{a})^{x}=\frac{1}{a^{x}}=a^{-x}$ なので, グラフ $y=a^{x}$ の $y$ 軸対称となっている. |
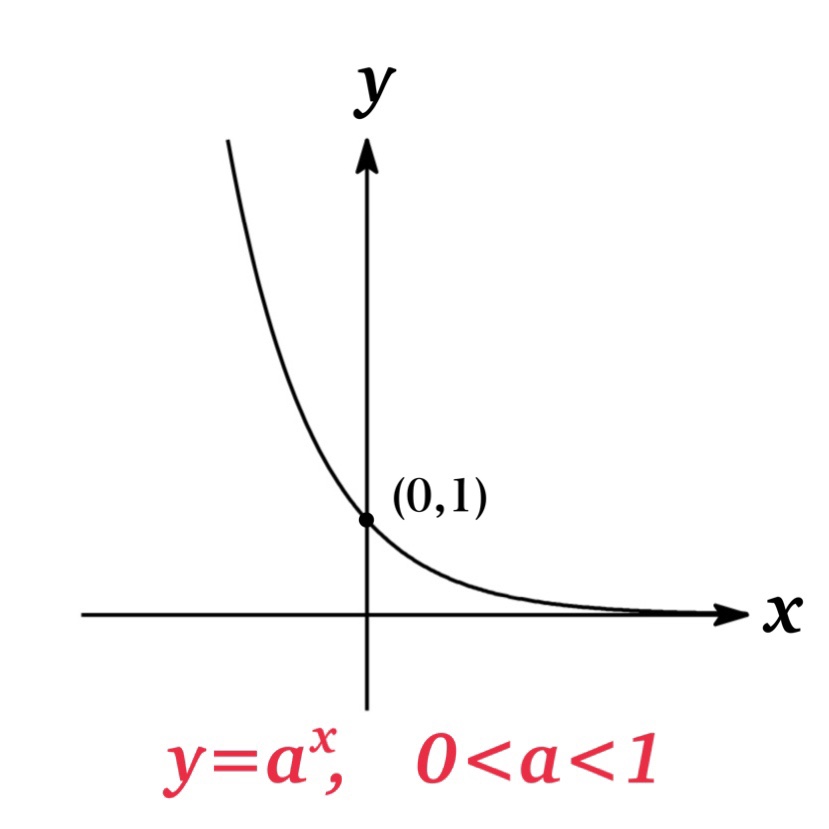
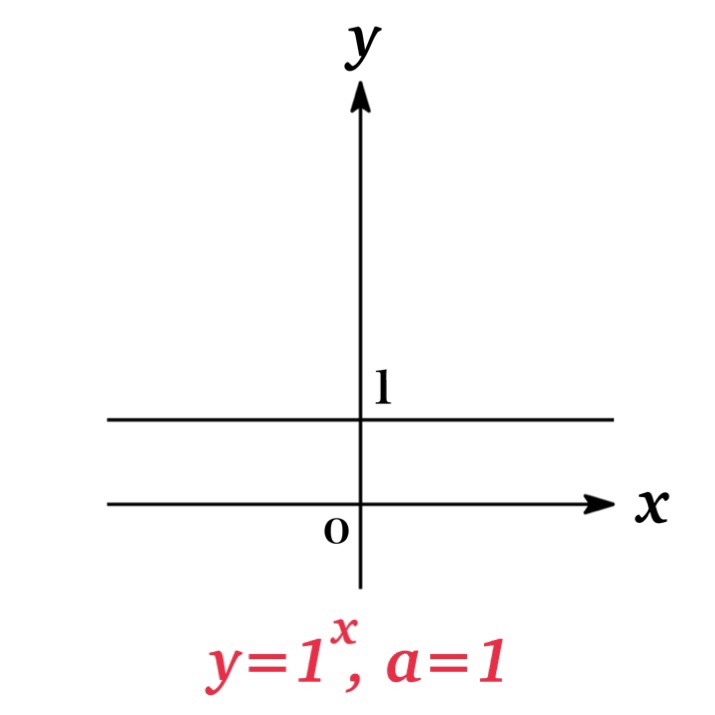
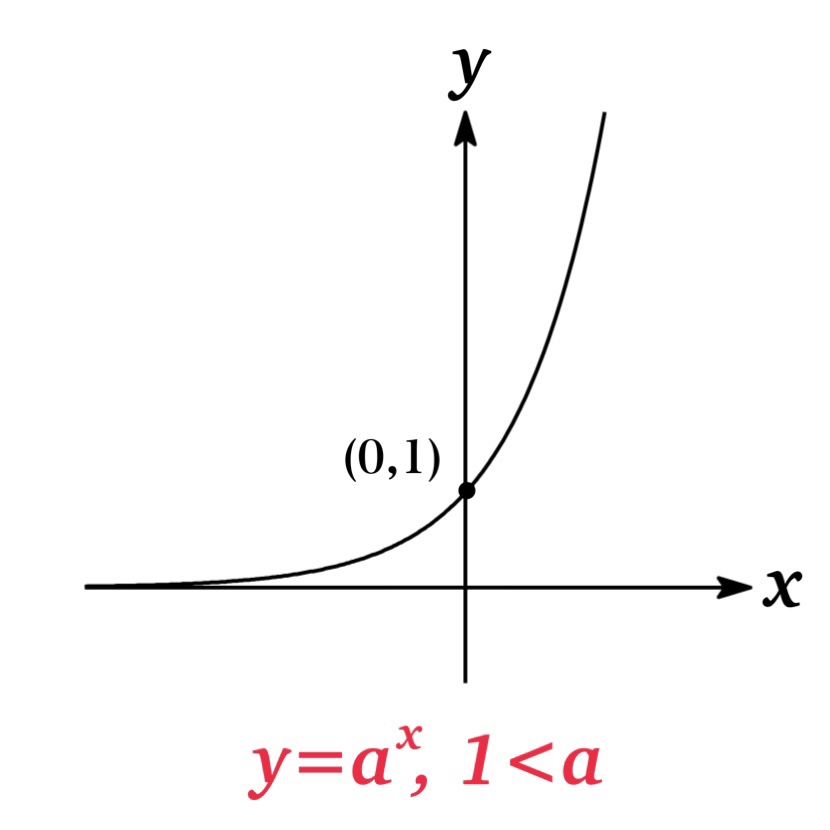
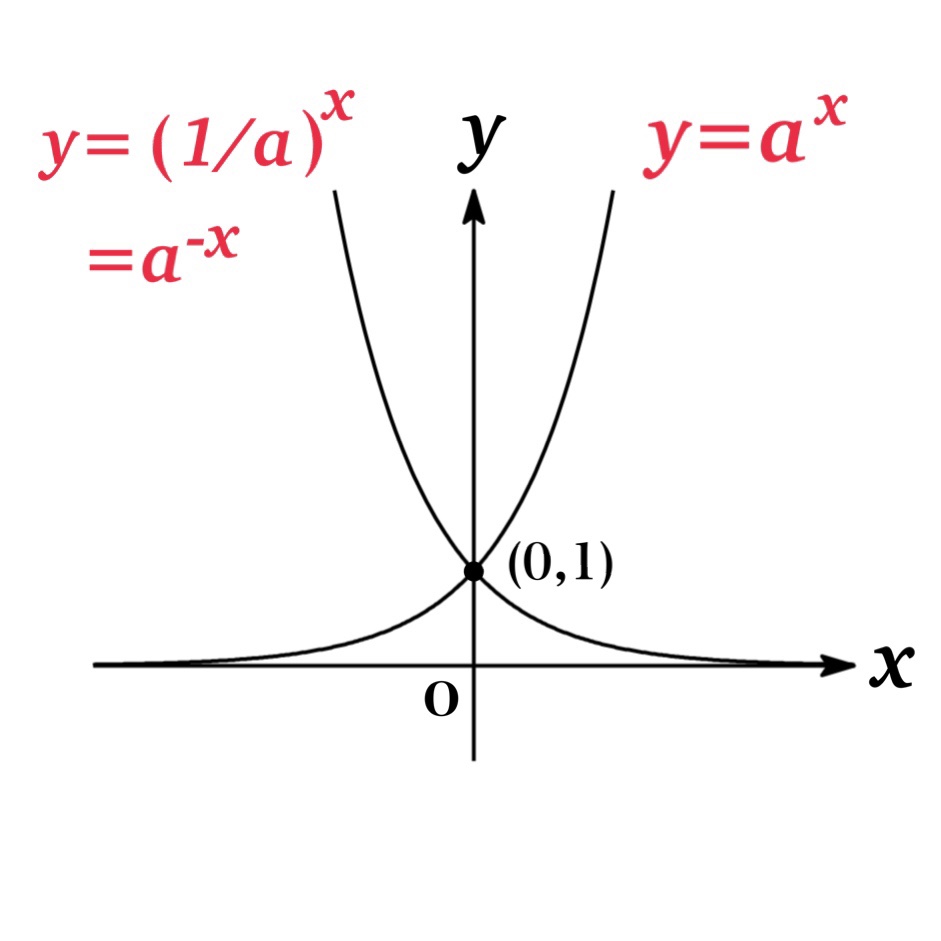
グラフからわかるように, $y=a^{x}$ のグラフは $(0,1)$ と $(1,a)$ を通り, $x$軸( $y=0$ )を漸近線とする. ただし $a=1$ の場合, グラフは $y=1$ となるため, $x$ 軸は漸近線とならない.
逆関数
$a>0$ かつ $a\not=1$ とする.
このとき, 指数関数 $y=a^{x}$ の逆関数は $a$ を底とする対数関数 $y=\log_{a} x$ で定義される.
$$\log_{a} x=y\ \ \ \ \Longleftrightarrow a^{y}=x$$
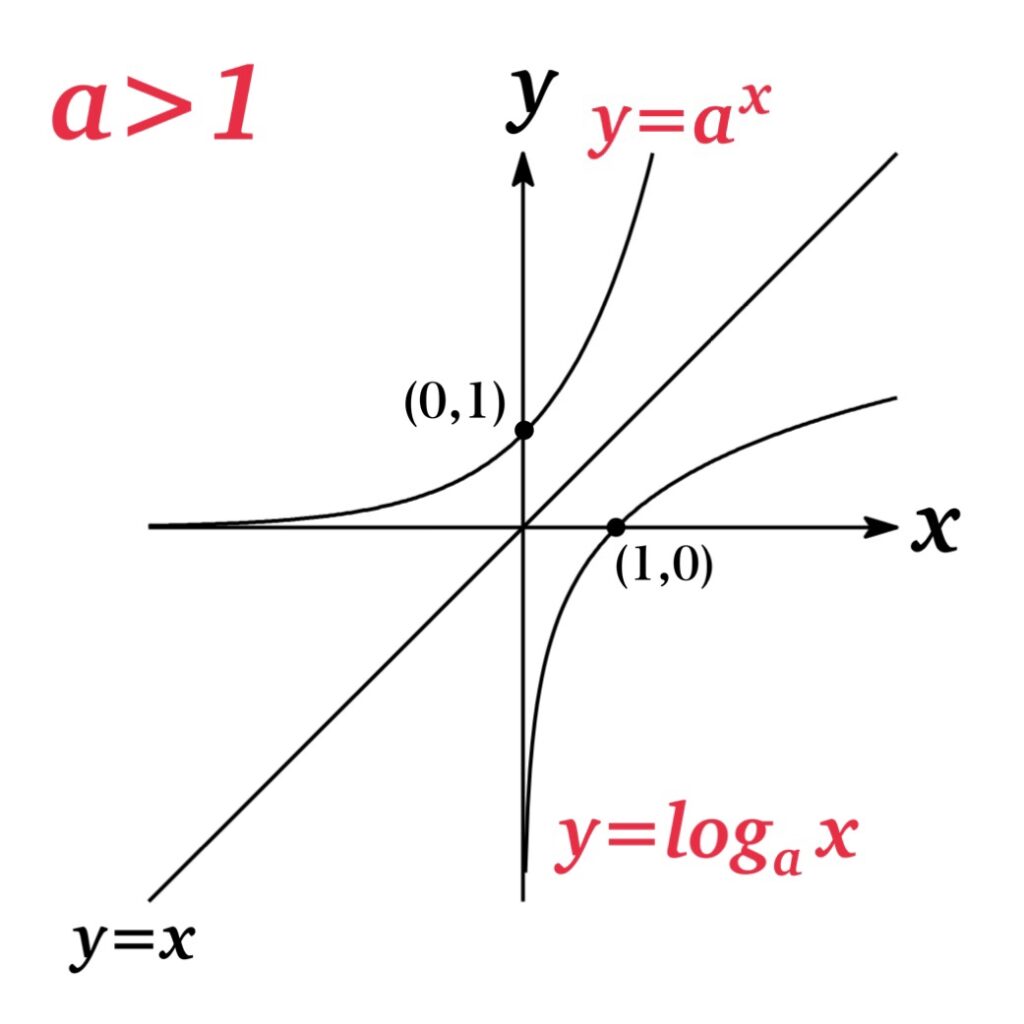
Notice1 :$a>0$ かつ $a\not=1$ より, 指数関数 $y=a^{x}$ のグラフは単調増加または単調減少グラフとなるため, 逆関数を定義することができる.
Notice2: 逆関数の性質より, 指数関数 $y=a^{x}$ のグラフは対数関数 $y=\log_{a}x$ のグラフを直線 $y=x$ に関して対称移動したものとなる.
導関数
$$\frac{d}{dx}[a^{x}]=a^{x}\log_{e} a $$
証明:底の変換公式 $\mathrm{e}^{\log_{e} a}=a$ を用いて微分する:
$\begin{eqnarray*}\frac{d}{dx}(a^{x})&=&\frac{d}{dx}(\mathrm{e}^{\log_{e} a})^{x}\\&=&\frac{d}{dx}\mathrm{e}^{(\log_{e} a)x}\\&=&\mathrm{e}^{(\log_{e} a)x}\frac{d}{dx}(\log_{e} a)x\\&=&(\mathrm{e}^{\log_{e} a})^{x}(\log_{e}a)\\&=&a^{x}\log_{e} a\end{eqnarray*}$
別証明:導関数の定義に従い証明する:
$\begin{eqnarray*}\frac{d}{dx}a^{x}&=&\displaystyle\lim_{h\rightarrow 0}\frac{a^{x+h}-a^{x}}{h}\\&=&\displaystyle\lim_{h\rightarrow 0}\frac{a^{x}(a^{h}-1)}{h}\\&=&a^{x}\displaystyle\lim_{h\rightarrow 0}\frac{(a^{h}-1)}{h}\end{eqnarray*}$
ここで $a^{h}-1=t \left( \text{ すなわち } \log_{e} a^{h}=\log_{e} (1+t)\right)$とおくと
$h\rightarrow 0$ のとき $t\rightarrow 0$ となる.
このとき $h=\frac{\log_{e} (1+t)}{\log_{e} a}$ であることに注意すれば
$\begin{eqnarray*}\text{(与式)} &=&a^{x}\displaystyle\lim_{t\rightarrow 0}\frac{t}{\frac{\log_{e} (1+t)}{\log_{e} a}}\\&=&(a^{x}\log_{e} a)\displaystyle\lim_{t\rightarrow 0}\frac{t}{\log_{e}(1+t)}\\&=&(a^{x}\log_{e} a)\displaystyle\lim_{t\rightarrow 0}\frac{1}{\frac{\log_{e}(1+t)}{t}}\text{(*)}\\&=&a^{x}\log_{e}a\end{eqnarray*}$
(*)上式の証明には $\displaystyle\lim_{t\rightarrow 0}\frac{\log_{e}(1+t)}{t}=1$ を用いた. → 証明
不定積分
$$\int a^{x}\ dx=\frac{a^{x}}{\log_{e} a}+C$$
証明: $\frac{d}{dx}[a^{x}]=a^{x}\log_{e} a $ より明らか.