双曲線関数 \(\sinh x,\ \cosh x,\ \tanh x\) を次で定める.
$\begin{eqnarray*}\sinh x&=&\frac{e^{x}-e^{-x}}{2}\ \ \ \ \ \text{( hyperbolic sine:ハイパボリック・サイン )}\\\cosh x&=&\frac{e^{x}+e^{-x}}{2}\ \ \ \ \ \text{( hyperbolic cosine:ハイパボリック・コサイン )}\\\tanh x&=&\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\ \ \ \ \ \text{( hyperbolic tangent:ハイパボリック・タンジェント )}\end{eqnarray*}$
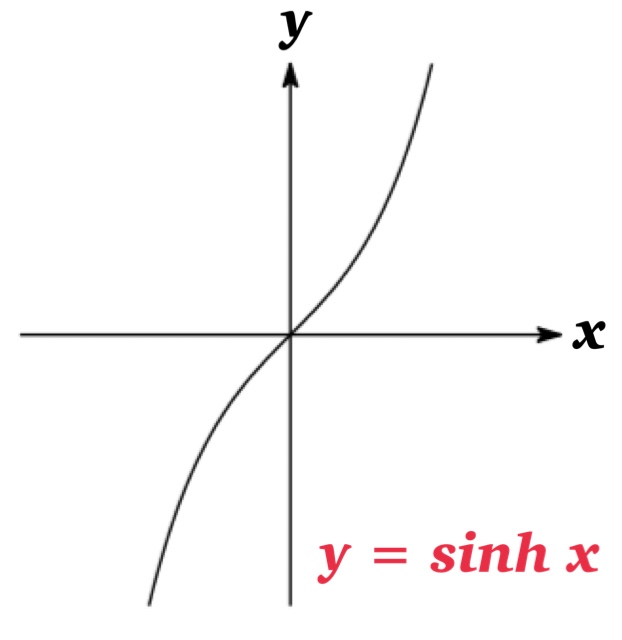
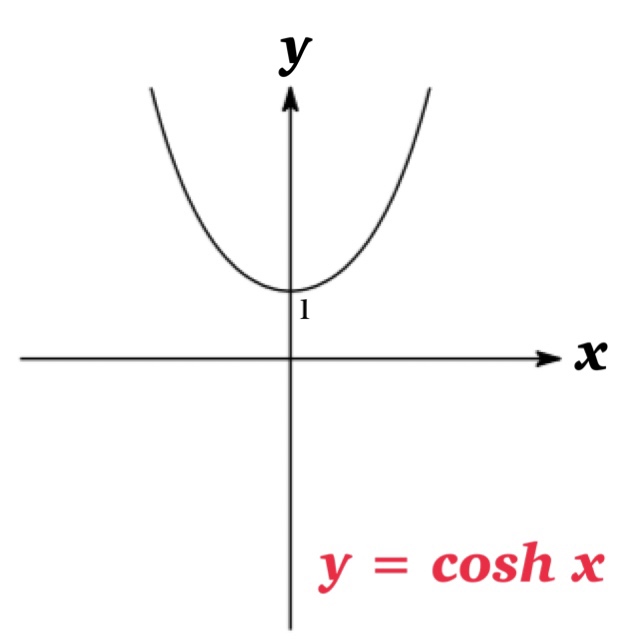
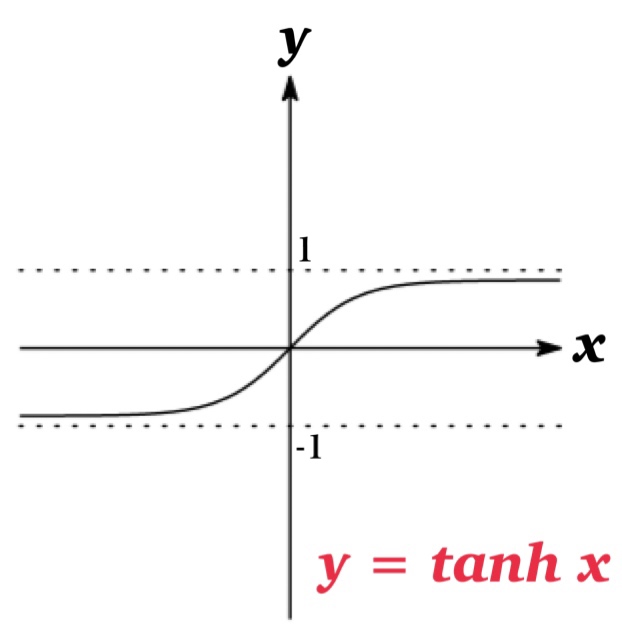
双曲線関数は三角関数と類似した性質をいくつも満たすことでよく知られいる.
また $(x,y)=(\cosh t, \sinh t)$ とした場合, \(\cosh^{2} t-\sinh^{2} t=1\)より\(x^{2}-y^{2}=1\)となることより「双曲線」関数と呼ばれる.
また三角関数の$\sin x,\ \cos x,\ \tan x$ の逆数: $\mathrm{cosec} x, \mathrm{sec} x, \mathrm{cot} x$ と同様, 双曲線関数においても次のように逆数が定義される:
\(\mathrm{csch} x,\ \mathrm{sech} x,\ \mathrm{coth} x\) を次で定める:
$$\begin{eqnarray*}\mathrm{csch}\ x&=&\frac{1}{\sinh x} \\\mathrm{sech}\ x&=&\frac{1}{\cosh x} \\\mathrm{coth}\ x&=&\frac{1}{\tanh x}\end{eqnarray*}$$
Contents
三角関数との類似点
双曲線関数は三角関数が満たす同様の性質も持っている.
偶関数・奇関数
| 双曲線関数 | 三角関数 | 偶奇性 |
| \(\sinh (-x)=-\sinh x\) | \(\sin (-x)=-\sin x\) | 奇関数 |
| \(\cosh (-x)=\cosh x\) | \(\cos (-x)=\cos x\) | 偶関数 |
| \(\tanh (-x)=-\tanh x\) | \(\tan (-x)=-\tan x\) | 奇関数 |
基本公式
| 双曲線関数 | 三角関数 |
| \(\tanh x=\frac{\sinh x}{\cosh x}\) | \(\tan x=\frac{\sin x}{\cos x}\) |
| \(\cosh^{2} x-\sinh^{2} x=1\) | \(\sin^{2} x+\cos^{2} x=1\) |
| \(1-\tanh^{2} x=\frac{1}{\cosh^{2} x}\) | \(1+\tan^{2} x=\frac{1}{\cos^{2} x}\) |
加法定理
| 双曲線関数 | 三角関数 |
| \(\sinh (x+ y)=\sinh x\cosh y+ \cosh x\sinh y\) | \(\sin (x+ y)=\sin x\cos y+ \cos x\sin y\) |
| \(\cosh (x + y)=\cosh x\cosh y+ \sinh x\sinh y\) | \(\cos (x + y)=\cos x\cos y- \sin x\sin y\) |
| \(\tanh (x + y)=\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}\) | \(\tan (x + y)=\frac{\tan x+\tan y}{1-\tan x\tan y}\) |
上記の式において, $y$ に $-y$ を代入することで, \(\sinh (x- y), \cosh (x-y)\), \(\tanh (x-y)\) の公式を得る.
例 : \(\sinh \left(x+ (-y)\right)=\sinh x\cosh (-y)+ \cosh x\sinh (-y)=\sinh x\cosh y- \cosh x\sinh y\)
微分公式
| 双曲線関数 | 三角関数 |
| \((\sinh x)’=\cosh x\) | \((\sin x)’=\cos x\) |
| \((\cosh x)’=\sinh x\) | \((\cos x)’=-\sin x\) |
| \((\tanh x)’=\frac{1}{\cosh^{2} x} \) | \((\tan x)’=\frac{1}{\cos^{2} x}\) |
| \((\mathrm{csch}\ x)’=-\mathrm{csch}\ x \cdot\mathrm{coth}\ x\) | \((\mathrm{csc}\ x)’=-\mathrm{csc}\ x \cdot\mathrm{cot}\ x\) |
| \((\mathrm{sech}\ x)’=-\mathrm{sech}\ x \cdot\mathrm{tanh}\ x\) | \((\mathrm{sec}\ x)’=\mathrm{sec}\ x \cdot\mathrm{tan}\ x\) |
| \((\mathrm{coth}\ x)’=-\mathrm{csch}^{2}\ x\) | \((\mathrm{cot}\ x)’=-\mathrm{csc}^{2}\ x\) |
積分公式
双曲線関数の微分公式より, 次の積分公式が得られる:
| 双曲線関数 | 三角関数 |
| \(\int \sinh x\ dx=\cosh x +C\) | \(\int \sin x\ dx=-\cos x +C\) |
| \(\int \cosh x\ dx=\sinh x +C\) | \(\int \cos x\ dx=\sin x +C\) |
| \(\int \tanh x\ dx=\ln \cosh x +C\) | \(\int \tan x\ dx=\ln |\sec x| +C\) |
| \(\int \mathrm{csch}\ x\ dx=\ln |\tanh \frac{x}{2}|+C\) | \(\int \csc x\ dx=\ln |\csc x-\cot x|+C\) |
| \(\int \mathrm{sech}\ x\ dx=\tan^{-1}|\sinh x|+C\) | \(\int \sec x\ dx=\ln |\sec x+\tan x|+C\) |
| \(\int \coth x\ dx=\ln |\sinh x|+C\) | \(\int \cot x\ dx=\ln |\sin x|+C\) |
三角関数と双曲線関数の関係性
$\sin x$ と $\cos x$ を双曲線関数を使うと次のように表される:$$\sin x=-i\sinh ix\ \ \ \ \ \cos x=\cosh ix$$
上記の式はオイラーの公式( \(\mathrm{e}^{ix}=\cos x+i\sin x\))より得られる.
オイラーの公式において $x$ を $-x$ に置き換えると, \(\mathrm{e}^{-ix}=\cos x-i\sin x \ \ \ (*)\).
このとき, オイラーの公式と $(*)$ より次を得る:
$$\sin x=\frac{\rm{e}^{ix}-\rm{e}^{-ix}}{2i}\ \ \ \ \ \cos x=\frac{\rm{e}^{ix}+\rm{e}^{-ix}}{2}$$
これらの関係性より, 三角関数と双曲線関数は似たような性質をもつ.
ただし関係式に含まれる虚数 $i$ によって符号(±)に違いが生じる.
「双曲線」関数と呼ばれる理由
このとき \(\cosh^{2} t-\sinh^{2} t=1\)より, 双曲線 \(x^{2}-y^{2}=1\)となる.
グラフの概形
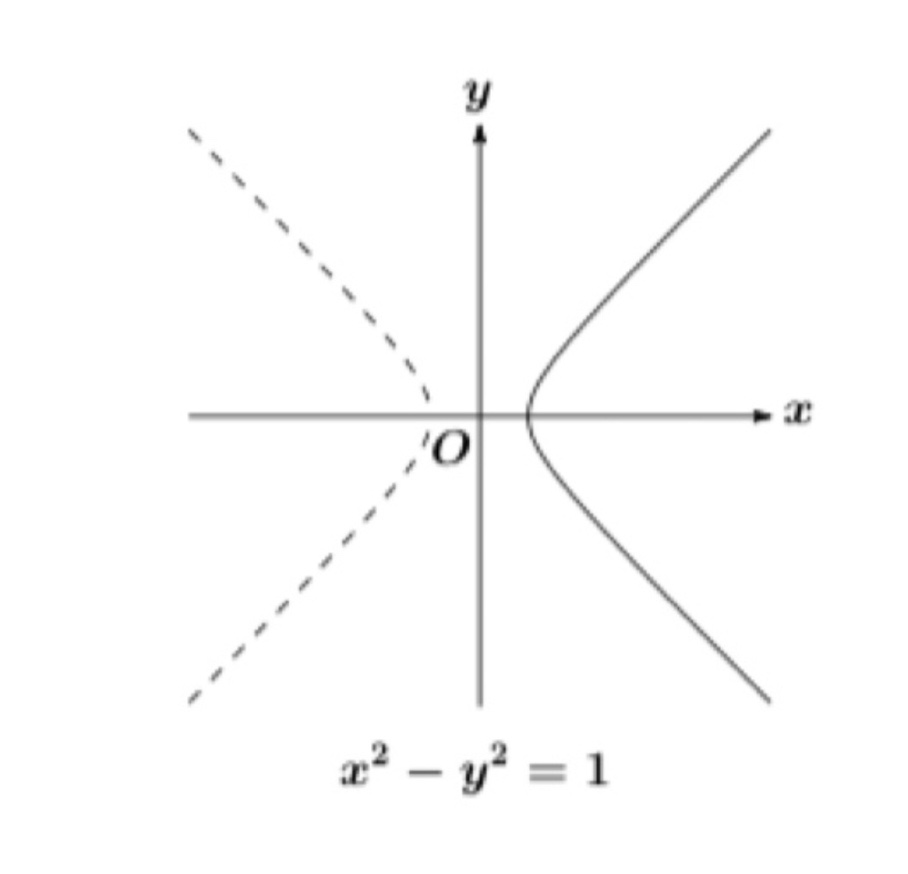
注意:\(x^{2}-y^{2}=1\) 自体は \(x<0\) においてもグラフは存在するが(点線部分), \(\ x\) の定義域は \(x>0 \ (\cosh t=\frac{e^{t}+e^{-t}}{2}>0) \)となっているため \(x^{2}-y^{2}=1\) のグラフの右半分となる.
関連記事
- 三角関数
- 逆双曲線関数