関数 $f(x)$ を単調増加または単調減少関数(すなわち $1:1$ )であるとする.
このとき ある $y$ に対してある $x$ がただ一つ定まる. これを $x=f^{-1}(y)$ と表し, $f^{-1}$ を$f$ の逆関数という. すなわち
$$y=f(x) \ \ \Longleftrightarrow \ \ x=f^{-1}(y)$$
ある関数 $f(x)$ に対して, 逆関数 $f^{-1}(x)$ はそれを元に戻す関数である.
すなわち
$$x\overset{f}{\longrightarrow}\ \ y=f(x) \ \ \overset{f^{-1}}{\longrightarrow}\ \ f^{-1}(y)=x$$
注意:$f^{-1}(x)\not= \frac{1}{f(x)}$ である.
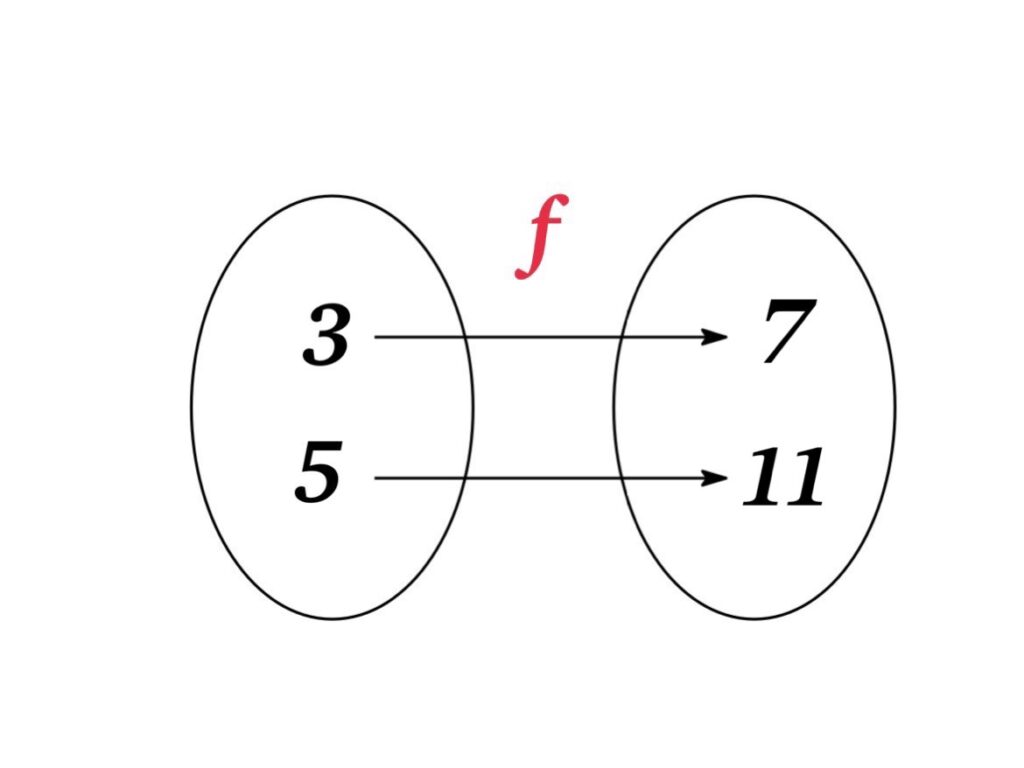
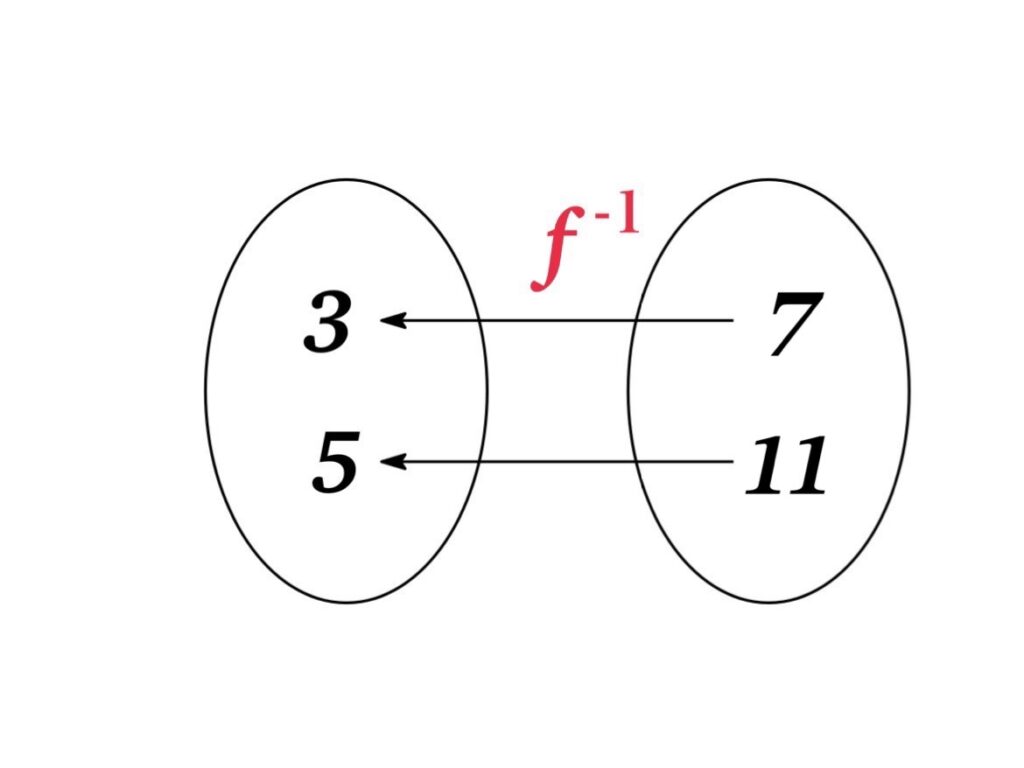
Example: $f(x)=2x+1$ の場合, 逆関数の対応は次のようになる:
- $f(3)=7$ に対して, $f^{-1}(7)=3$
- $f(5)=11$ に対して, $f^{-1}(11)=5$
ショートコード
関数 $f : X\longrightarrow Y$ に対して, 逆関数は $f^{-1}: Y\longrightarrow X$ となることより, 定義域と値域が入れ替わることは明らか.
\begin{eqnarray*}&&f^{-1} \text{ の定義域}= f\text{ の値域}\\&&f^{-1}\text{ の値域} = f\text{ の定義域}\end{eqnarray*}
なぜ単調関数である必要があるのか?
逆関数を定義する上で単調関数 (1:1) であることが条件であるように, すべての関数が逆関数をもつわけではない.
もし関数が単調関数 (1:1) でない場合はどうなるかを考えてみる.
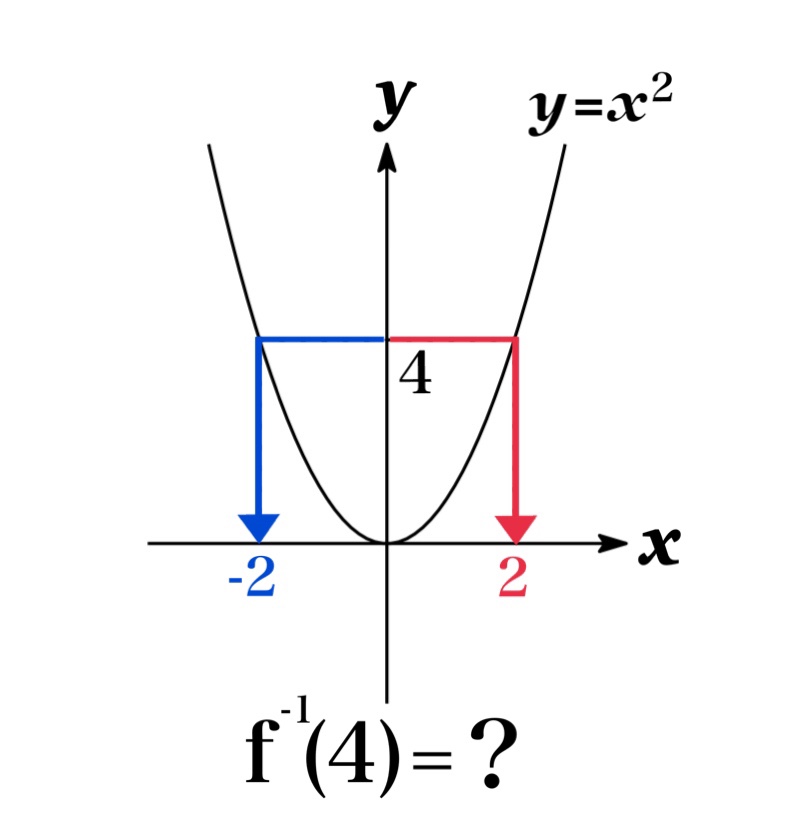
例えば, 関数 $f(x)=x^{2}$ の場合, $f(x)=x^{2}$ は単調関数(1:1)でないため, 逆関数をもたない.
なぜなら, $f(x)=x^{2}$ を満たす $x$ が一意に定まらない. (すなわち, $f(x)=f(-x)=x^{2}$. Fig.1 参照 )
よって 逆関数 $f^{-1}$ の写像の行先が定まらないため, 逆関数を定義することができない.
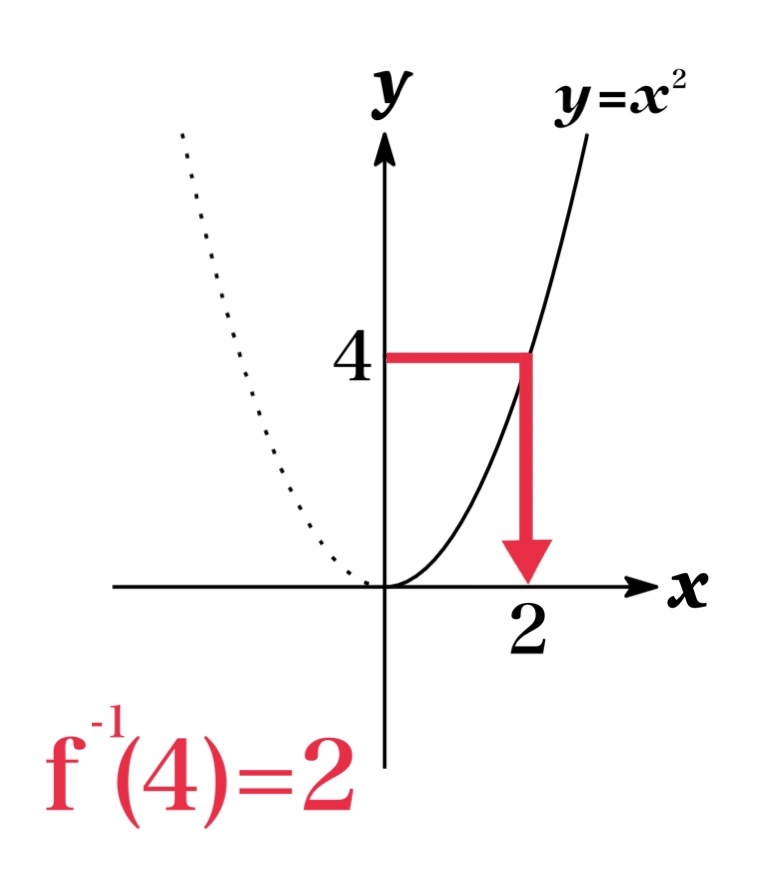
注意:ただし $x$ の定義域を $x\geq 0$ に制限すれば, $f(x)=x^{2}$ は単調関数となるため, 逆関数を定義することが可能となる. (図2参照)
逆関数の求め方
(Step 1) 与えられた関数 $f(x)$ を $y=f(x)$ で表す.
(Step 2) $y=f(x)$ を $x$ について解く. すなわち $x=g(y)$ の形に変形する.
(Step 3) $x$ と $y$ を入れ替え, $y=g(x)=f^{-1}(x)$ とする.
得られた $y=f^{-1}(x)$ が 関数 $f(x)$ の逆関数となる.
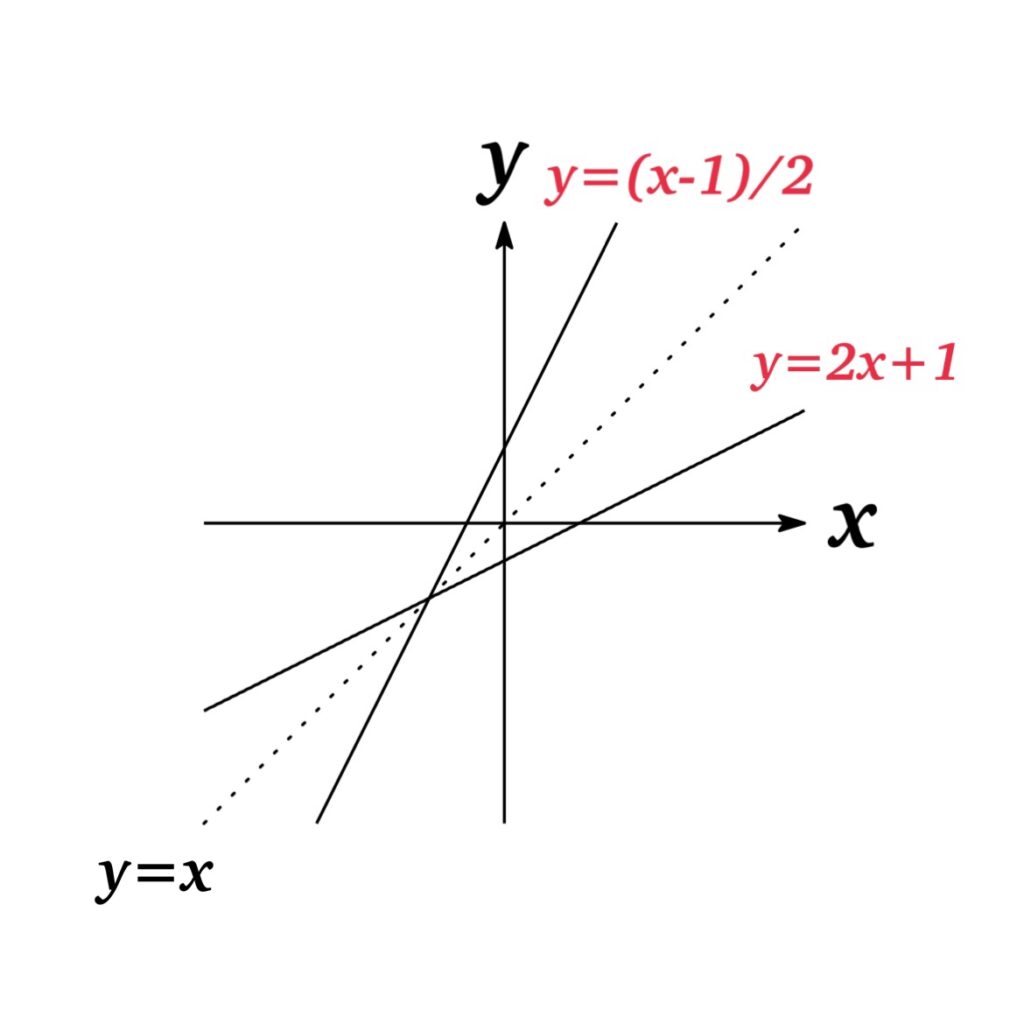
$\fbox{例題}$:$f(x)=2x+1$ の逆関数を求めよ.
(Step 1) 与えられた関数 \(f(x)=2x+1\) を次の形で表す:
$$y=2x+1$$
(Step 2) $x$ について解く:
\begin{eqnarray*}2x&=&y-1\\x&=&\frac{y-1}{2}\end{eqnarray*}
(すなわち $x=g(y)=\frac{y-1}{2}$.)
(Step 3) $x$ と $y$ を入れ替える:
$$y=\frac{x-1}{2}$$
よって$f(x)=2x+1$ の逆関数は $f^{-1}(x)=\frac{x-1}{2}$ となる.
グラフ
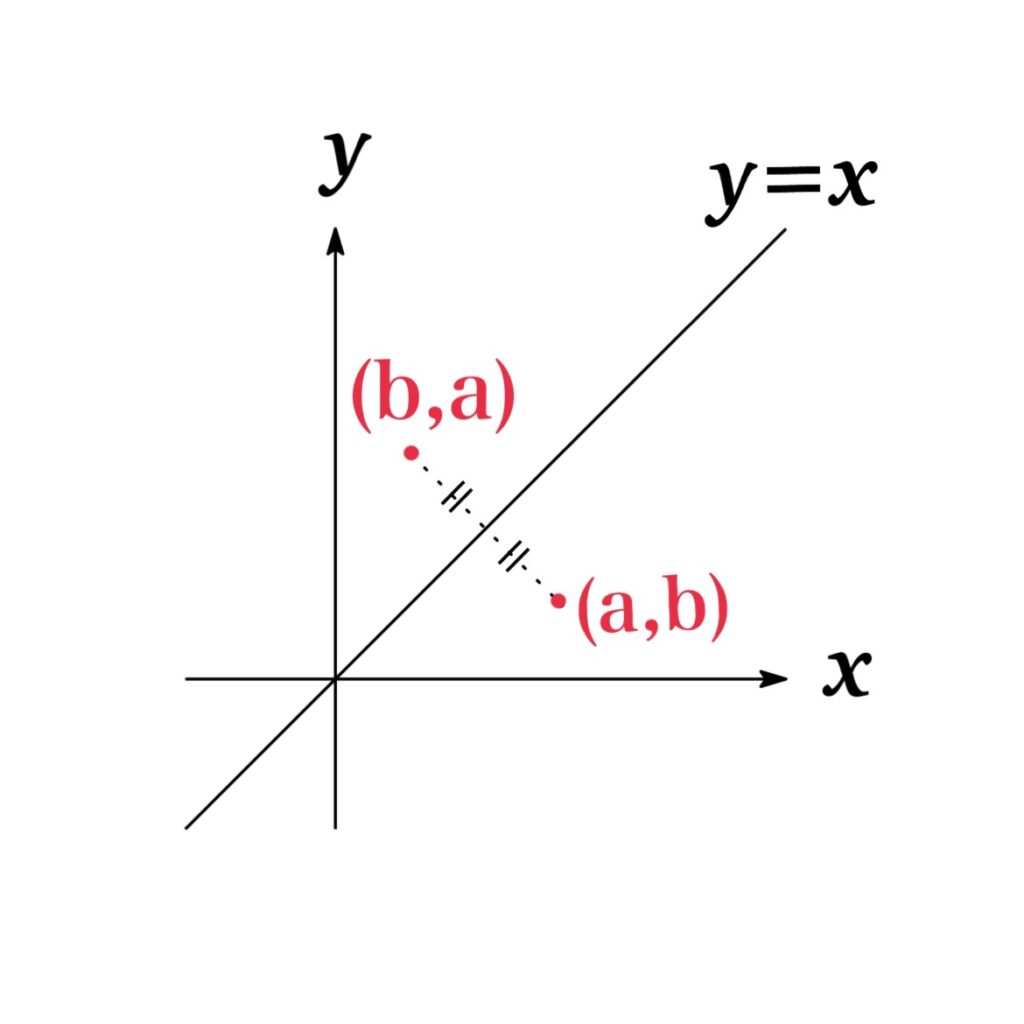
関数 $f(x)$ とその逆関数 $f^{-1}(x)$ のグラフは $y=x$ に関して対称となる.
$y=x$ に関して対称となる理由を考える.
逆関数の定義より, $y=f(x)$ であるとき逆関数は $f^{-1}(y)=x$ である.
すなわち関数 $f(x)$ 上の任意の点 が $(a,b)$ (i.e. $f(a)=b$) となるとき, 逆関数上の点 は$(b,a)$ (i.e. $f^{-1}(b)=a$)となる.
また点 $(a,b)$ と $(b,a)$ は $y=x$ に関して対称であることに留意すれば, $f(x)$ と $f^{-1}(x)$ のグラフは $y=x$ に関して対称となることがわかる.
導関数
関数 $y=f(x)$ は微分可能であるとする. このとき逆関数 $f^{-1}(x)$ が存在するとき
$$\frac{d}{dx}f^{-1}(x)=\frac{dy}{dx}=\frac{1}{\ \frac{dx}{dy}\ }=\frac{1}{f'(y)}$$
ただし $f'(y)\not=0$ とする.
逆関数 $y=f^{-1}(x)$ を $x=f(y)$ と表す.
このとき $x=f(y)$ の両辺を $x$ で微分すれば, 合成関数の微分法より
$$1=f'(y)\cdot y’=f'(y)\cdot \frac{d}{dx}f^{-1}(x)$$
$f'(y)=\frac{dx}{dy}\not= 0$ であれば
$$\frac{d}{dx}f^{-1}(x)=\frac{1}{f'(y)}=\frac{1}{\frac{dx}{dy}}$$
例
$f(x)=x^{2}\ (x\geq 0)$ の逆関数の導関数を求めよ.
解答 : $f'(x)=\frac{d}{dx}f(x)=2x$, $f^{-1}(x)=\sqrt{x}$ より
$$\frac{d}{dx}f^{-1}(x)=\frac{1}{f'(y)}=\frac{1}{2y}=\frac{1}{2f^{-1}(x)}=\frac{1}{2\sqrt{x}}$$
$f(x)=x^{3}+3x^{2}+6x$ の逆関数を $g(x)$ とするとき, 微分係数 $g'(10)$ を求めよ.
解答 : $y=x^{3}+3x^{2}+6x$ の逆関数は $x=y^{3}+3y^{2}+6y$ で表されるので, 両辺を $y$ で微分すると
$$\frac{dx}{dy}=3y^{2}+6y+6$$
よって
$$g'(x)=\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{3y^{2}+6y+6}$$
$x=10$ のとき $10=y^{3}+3y^{2}+6y$ を解くと
$$(y-1)(y^{2}+4y+10)=0$$
$y=1$ となるので $g(10)=1$. よって
$$g'(10)=\frac{1}{3\cdot 1^{2}+6\cdot 1+6}=\frac{1}{15}$$