関数 $f(x)$ の テイラー展開における $n$ 次までの有限和:
$$f_{n}(x):=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f”(a)}{2!}(x-a)^{2}+\cdots +\frac{f^{n}(a)}{n!}(x-a)^{n}$$
を $x=a$ における $n$ 次のテイラー多項式という.
$f_{n}(x)$ は テイラー展開による関数 $f(x)$ の $ n$ 次近似となっている.
($ a=0$ でのテイラー展開の場合: $f_{n}(x)=\displaystyle \sum_{k=0}^{n} \frac{f^{(n)}(0)}{k!}x^{k}$ はマクローリン多項式と呼ばれる. )
また $n$ が大きくなるにつれて $f_{n}(x)$ が $f(x)$ のよい近似になることは明らかである. すなわち
$$\displaystyle\lim_{n\rightarrow \infty} f_{n}(x)=f(x)$$
例
指数関数 $f(x)=\mathrm{e}^{x}$ の場合, 1, 2, 3 次のマクローリン多項式 ($x=0$ でのテイラー多項式) を求めよ
指数関数 $f(x)=\mathrm{e}^{x}$ の場合, 1, 2, 3 次のマクローリン多項式 ($x=0$ でのテイラー多項式) は次で与えられる.
$$f_{1}(x)=1+x,\ \ f_{2}(x)=1+x+\frac{x^{2}}{2!}, \ \ f_{3}(x)=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}$$
指数関数 $f(x)=\mathrm{e}^{x}$ と 1次, 2次, 3 次の多項式 のグラフは以下のようになる.

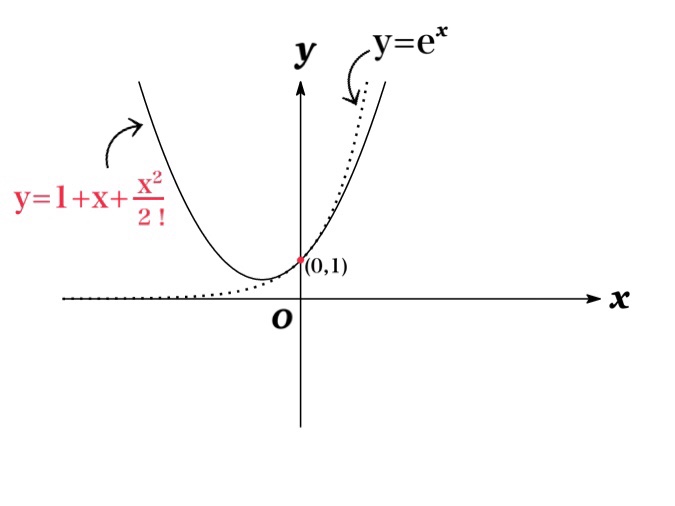

グラフより $n$ が大きくなるにつれて, $f_{n}(x)$ が $f(x)=\mathrm{e}^{x}$に近づいていることがわかる.
実際の計算における近似
マクロリーン展開を用いて \((1.00005)^{17}\) を1次近似せよ.
$f(x)=(1+x)^{17}$とする. このとき
$$(1.00005)^{17}=(1+0.00005)^{17}=f(0.00005)$$
マクロリーン展開($x=0$ におけるテイラー展開)により
$$f(x)=(1+x)^{17}=_{17}\mathrm{C}_{0}+_{17}\mathrm{C}_{1}x+_{17}\mathrm{C}_{2}x^{2}+\cdots +_{17}\mathrm{C}_{k}x^{k}+\cdots$$
これより1次マクローリン多項式は以下のように与えられる:
$$f(x)=(1+x)^{17}\approx \ _{17}\mathrm{C}_{0}+_{17}\mathrm{C}_{1}x$$
よってマクローリン展開による次近似は
$$f(0.00005)=(1+0.0005)^{17}\approx \ _{17}\mathrm{C}_{0}+_{17}\mathrm{C}_{1} (0.00005)=1.00085$$
マクロリーン展開を用いて \(\sin 0.1\) を3次近似せよ.
このときマクロリーン展開をすれば
$$f(x)=\sin x=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\cdots +\frac{(-1)^{k}}{(2k+1)!}x^{2k+1}+\cdots$$
これより, 3次マクローリン多項式は以下で与えられる:
$$f(x)=\sin x\approx \ x-\frac{1}{3!}x^{3}$$
よってマクローリン展開による3次近似は
$$f(0.1)=\sin 0.1\approx \ 0.1-\frac{1}{3!}(0.1)^{3}=0.09983$$
「1次近似」と「グラフの接線」
$x=a$ におけるテイラー多項式による1次近似は次で与えられる:
$$f_{1}(x)=f(a)+f'(a)(x-a)$$
上式はよくご存知のように $x=a$ における $y=f(x)$ の接線と同式である:
$$y=f(a)+f'(a)(x-a)$$
グラフと接線は, 接線の近くでほぼ一致しているので, $x\approx a$ ならば $f(x) \approx f(a)+f'(a)(x-a)$ といえる.
すなわち, 接線は関数 $f(x)$ の1次近似といえる.
ただし 近似であるので, 誤差が生じることに注意する.
