不定形の極限値のおいて次が成立する.
$$\displaystyle\lim_{x\rightarrow a}\frac{g(x)}{f(x)}=\displaystyle\lim_{x\rightarrow a}\frac{g'(x)}{f'(x)}$$
たとえば $\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}$ のような極限値で分子分母のそれぞれの極限値が 0 となる場合, $\frac{0}{0}$ を不定形という. その他にも不定形には
$$\frac{\infty}{\infty},\ \ \ \infty\cdot 0,\ \ \ \infty-\infty$$
などの不定形も存在する. この等式は右辺の極限値 : $\displaystyle\lim_{x\rightarrow a}\frac{g'(x)}{f'(x)}$ が存在するならば, 左辺の極限値と等しくなることを意味する.
( NOTE 1 ) $\displaystyle\lim_{x\rightarrow a}\frac{g(x)}{f(x)}$ が不定形でない場合はロピタルの定理は成立しないので注意する.
( NOTE 2) $\displaystyle\lim_{x\rightarrow a}\frac{g'(x)}{f'(x)}$も不定形である場合は, ロピタルの定理を適用させれば $\displaystyle\lim_{x\rightarrow a}\frac{g'(x)}{f'(x)}=\displaystyle\lim_{x\rightarrow a}\frac{g”(x)}{f”(x)}$ が成立するので
$$\displaystyle\lim_{x\rightarrow a}\frac{g(x)}{f(x)}=\displaystyle\lim_{x\rightarrow a}\frac{g”(x)}{f”(x)}$$
が成立する. ( 不定形の極限ならば何度でもロピタルの定理が定理を適用できる. Exmple (2) を参照. )
( NOTE 3 ) またロピタルの定理は $\displaystyle\lim_{x\rightarrow a}$ が $\displaystyle\lim_{x\rightarrow +a}$, $\displaystyle\lim_{x\rightarrow -a}$, $\displaystyle\lim_{x\rightarrow \infty}$, $\displaystyle\lim_{x\rightarrow -\infty}$ の場合も成立する.
ロピタルの定理が使える例
(1) $\displaystyle\lim_{x\rightarrow 0}\frac{1-\cos x}{x}=\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{1}=0$ ( $\frac{0}{0}$ )
(2) $\displaystyle\lim_{x\rightarrow \infty} x^{3}e^{-x}=\displaystyle\lim_{x\rightarrow \infty}\frac{x^{3}}{e^{x}}=\displaystyle\lim_{x\rightarrow \infty}\frac{3x^{2}}{e^{x}}=\displaystyle\lim_{x\rightarrow \infty}\frac{6x}{e^{x}}=\displaystyle\lim_{x\rightarrow \infty}\frac{6}{e^{x}}=0$ ( $0\times \infty$ )
(3) $\displaystyle\lim_{x\rightarrow +0}x\log x=\displaystyle\lim_{x\rightarrow +0}\frac{\log x}{\frac{1}{x}}=\displaystyle\lim_{x\rightarrow +0}\frac{\frac{1}{x}}{-\frac{1}{x^{2}}}=\displaystyle\lim_{x\rightarrow +0}(-x)=0$ ( $(+0)\times (-\infty) $ )
(4) $\displaystyle\lim_{x\rightarrow ( \frac{\pi}{2}^{-} )} \frac{1}{\cos x}-\tan x=\displaystyle\lim_{x\rightarrow ( \frac{\pi}{2}^{-} )}\frac{1-\sin x}{\cos x}=\displaystyle\lim_{x\rightarrow ( \frac{\pi}{2}^{-} )}\frac{-\cos x}{-\sin x}=0$ ( $ \infty-\infty $)
与えられた式が分数形でない場合は, 分数形に変形すれば良い.
ロピタルの定理が使えない例
$\displaystyle\lim_{x\rightarrow a}\frac{g(x)}{f(x)}$ が不定形でない場合
$\displaystyle\lim_{x\rightarrow 0} \frac{x}{e^{x}}$ は 不定形でないのでそのまま計算すれば $\displaystyle\lim_{x\rightarrow 0} \frac{x}{e^{x}}=\frac{0}{1}=0$ を得るが, ロピタルの定理も用いた場合
$$\displaystyle\lim_{x\rightarrow 0} \frac{x}{e^{x}}=\displaystyle\lim_{x\rightarrow 0} \frac{1}{e^{x}}=\frac{1}{1}=1\not= 0$$
となり, 正しい極限値が得られないことがわかる.
$\displaystyle\lim_{x\rightarrow a}\frac{g'(x)}{f'(x)}$ が存在しない場合
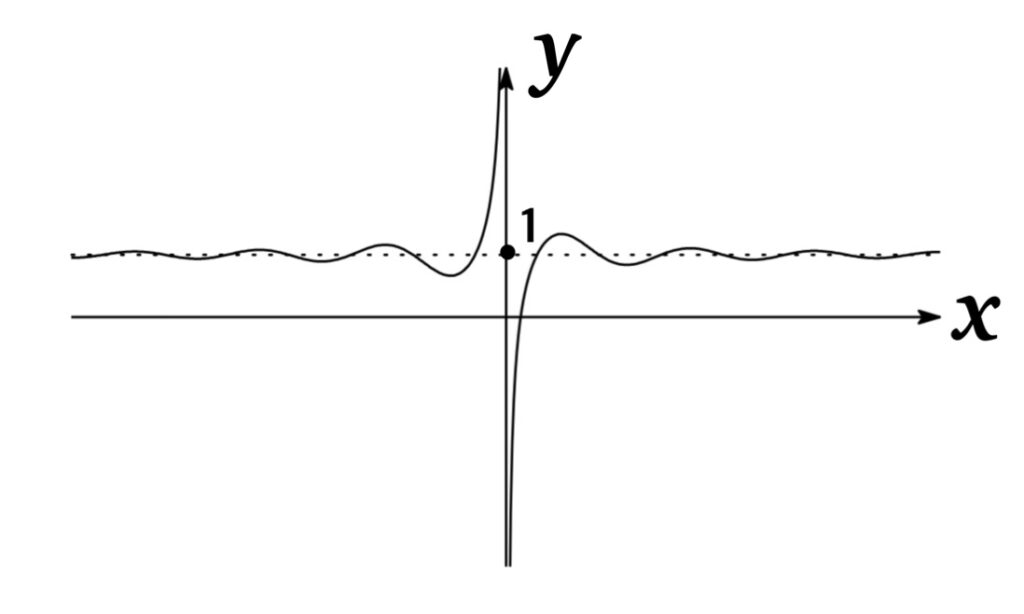
$\displaystyle\lim_{x\rightarrow \infty} \frac{x-\cos x}{x}$ は $\frac{\infty}{\infty}$ の不定形なので, ロピタルの定理を用いると $\displaystyle\lim_{x\rightarrow \infty} \frac{1+\sin x}{1}$ となり振動する.
ただしこのケースでは $-\frac{1}{x}\leq -\frac{\cos x}{x}\leq \frac{1}{x}$ より, はさみうちの原理を用いれば 極限値が 1 に収束することがわかる.
証明概略
不定形 $\frac{0}{0}$ の場合をコーシーの平均値の定理を用いて証明する. $x$ が $a$ に十分近ければ $\displaystyle\lim_{x\rightarrow a} f(x)=\displaystyle\lim_{x\rightarrow a} g(x)=0$ より
$$\frac{g(x)}{f(x)}=\frac{g(x)-g(a)}{f(x)-f(a)}=\frac{g'(c)}{f'(c)}$$
となる $c$ が $a<c<x$ に存在する. よって $x\rightarrow a$ のとき, $c\rightarrow a$ より $\displaystyle\lim_{x\rightarrow a} \frac{g'(x)}{f'(x)}$ が存在すれば
$$\displaystyle\lim_{x\rightarrow a}\frac{g(x)}{f(x)}=\displaystyle\lim_{x\rightarrow a}\frac{g(x)-g(a)}{f(x)-f(a)}=\displaystyle\lim_{c\rightarrow a}\frac{g'(c)}{f'(c)}=\displaystyle\lim_{x\rightarrow a}\frac{g'(x)}{f'(x)}$$
が成立する.