実数 $\theta$ に対して, 次が成り立つ:
$$\mathrm{e}^{i\theta}=\cos \theta+i\sin \theta $$
これをオイラーの公式またはオイラーの恒等式という.
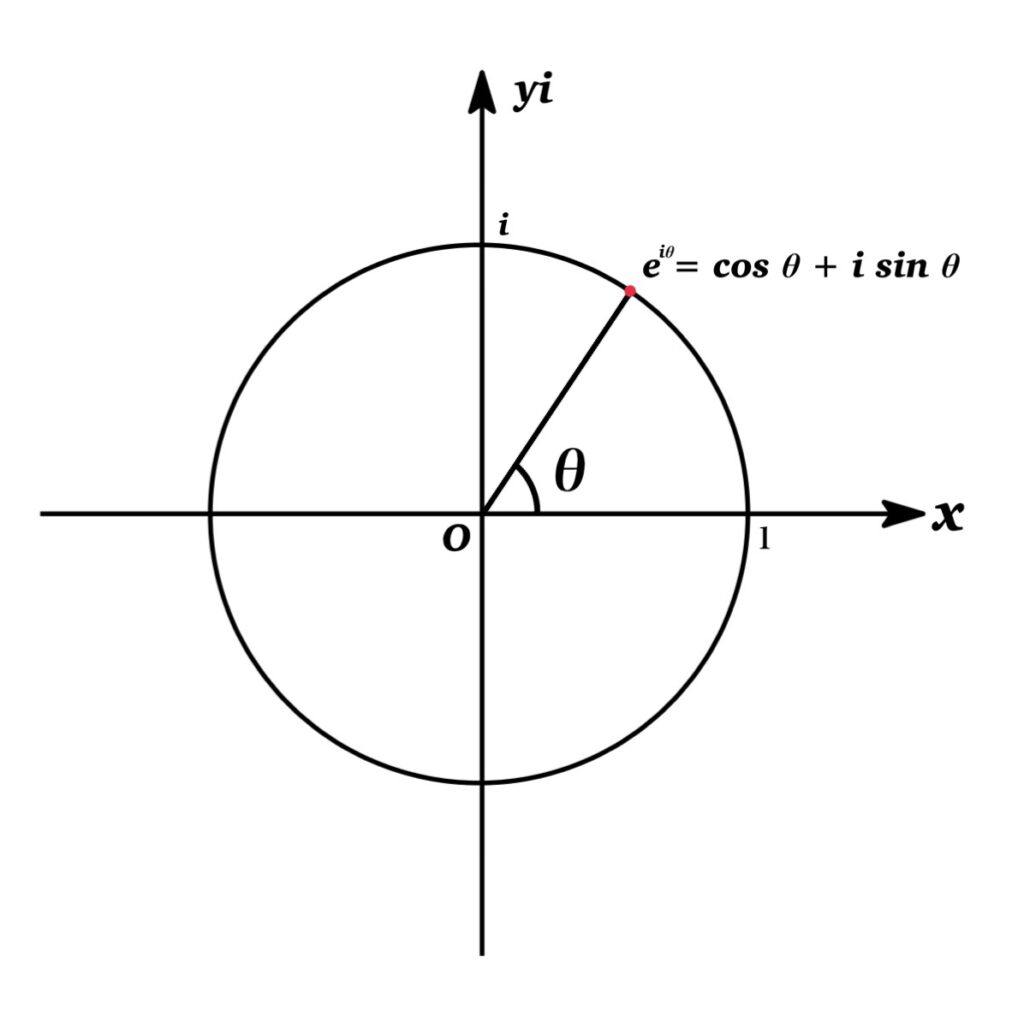
幾何的解釈
図が示すように, $\mathrm{e}^{i\theta}=cos\theta+i\sin \theta$ の表す点は 複素平面上において$(1,0)$ を角 $\theta$ だけ回転させた半径 $1$ の円周上にある.
オイラーの公式によって, ド・モアブルの定理が簡単に示される:
$$(\cos \theta+i\sin \theta)^{n}=(\mathrm{e}^{i\theta})^{n}=\mathrm{e}^{i(n\theta)}=\cos n\theta+i\sin n\theta$$
例
オイラーの公式において $\theta=\frac{\pi}{2},\ \pi,\ 2\pi$ のとき
- $\mathrm{e}^{i \frac{\pi}{2}}=\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}=0+i(1)=i$
- $\mathrm{e}^{i \pi}=\cos \pi+i \sin \pi=-1+i (0)=-1$
- $\mathrm{e}^{i 2\pi}=\cos 2\pi+i \sin 2\pi=1+i (0)=1$
証明
べき級数展開を用いた証明
$\mathrm{e}^{x},\ \cos x,\ \sin x$ をマクロリーン展開すると、次のようにべき級数展開される.
$$\begin{eqnarray*}&&\mathrm{e}^{x}=1+x^{}+\frac{1}{2!}x^{2}+\cdots +\frac{1}{k!}x^{k}+\cdots\\&&\sin x=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\cdots +\frac{(-1)^{k}}{(2k+1)!}x^{2k+1}+\cdots\\&&\cos x=1-\frac{1}{2!}x^{2}+\frac{1}{4!}x^{4}-\cdots +\frac{(-1)^{k}}{(2k)!}x^{2k}+\cdots\end{eqnarray*}$$
このとき $\mathrm{e}^{x}$ において、$x$ を $ix$ に置き換えると
$$\begin{eqnarray*}\mathrm{e}^{ix}&=&1+ix+\frac{1}{2!}{(ix)}^{2}+\frac{1}{3!}(ix)^{3}+\frac{1}{4!}(ix)^{4}\cdots +\frac{1}{k!}{(ix)}^{k}+\cdots\\&=&1+ix-\frac{1}{2!}x^{2}-\frac{1}{3!}ix^{3}+\frac{1}{4!}x^{4}+\cdots\\&=&\left(1-\frac{1}{2!}x^{2}+\frac{1}{4!}x^{4}-\cdots\right)+i\left(x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\cdots \right)\\&=&\cos x+i\sin x\end{eqnarray*}$$
よって $\mathrm{e}^{ix}=\cos x+i\sin x$ が成り立つことが証明された.
微分方程式を用いた証明
関数 $y=\mathrm{e}^{x},\ \cos x,\ \sin x$ はいずれも微分方程式
$$y^{(2)}+y=0$$
の解である. 2階線形微分方程式の独立解は2つしか存在しないので、解 $y=\mathrm{e}^{x},\ \cos x,\ \sin x$ の間に1次従属関係
$$\mathrm{e}^{ix}=a\cos x+b\sin x\ \cdots \ (\text{*}) $$
が成り立つ. (*)を微分すると
$$i\mathrm{e}^{ix}=-a\sin x+i\sin x \ \cdots (\text{**})$$
(*) と (**) に $x=0$ を代入すると
$$a=1,\ b=i$$
を得る. よって $\mathrm{e}^{ix}=\cos x+i\sin x $ が成り立つことが証明された.
Remark
オイラーの公式によって, 三角関数は $\mathrm{e}$ を用いて次のように表わすことができる:$$\sin x=\frac{\rm{e}^{ix}-\rm{e}^{-ix}}{2i}\ \ \ \ \ \cos x=\frac{\rm{e}^{ix}+\rm{e}^{-ix}}{2}$$
これらの等式はオイラーの公式によって導かれる:
- $\mathrm{e}^{ix}=\cos x+i\sin x$
- $\mathrm{e}^{-ix}=\cos x-i\sin x \ \ \ (*)$
2つめの式はオイラーの公式において, $x$ を $-x$ に置き換えにより得られる.
上の2つの等式の足し合わせにより次が得られる:
- $\mathrm{e}^{ix}+\mathrm{e}^{-ix}=2\cos x$
- $\mathrm{e}^{ix}-\mathrm{e}^{-ix}=2i\sin x$
よって
- $\sin x=\frac{\rm{e}^{ix}-\rm{e}^{-ix}}{2i}$
- $\cos x=\frac{\rm{e}^{ix}+\rm{e}^{-ix}}{2}$
特に $\frac{e^{x}-e^{-x}}{2}, \ \frac{e^{x}+e^{-x}}{2}$ の形式は双曲線関数 ( Hyperbolic functions ) として知られている:
- $\sinh x=\frac{e^{x}-e^{-x}}{2}$ (双曲線正弦関数; hyperbolic sine )
- $\cosh x=\frac{e^{x}+e^{-x}}{2}$ (双曲線余弦関数; hyperbolic cosine )
よって三角関数と双曲線関数には, 次のような関係式が導かれる:
$$\sin x=-i\sinh ix\ \ \ \ \ \cos x=\cosh ix$$
これらの関係式より, 三角関数と双曲線関数は似たような性質をもつことが知られている.