Definitions
We define hyperbolic functions, \(\sinh x, \cosh x\) and \( \tanh x\) as below:
\(\sinh x=\frac{e^{x}-e^{-x}}{2}\) ( hyperbolic sine )
\(\cosh x=\frac{e^{x}+e^{-x}}{2}\) ( hyperbolic cosine )
\(\tanh x=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\) ( hyperbolic tangent )
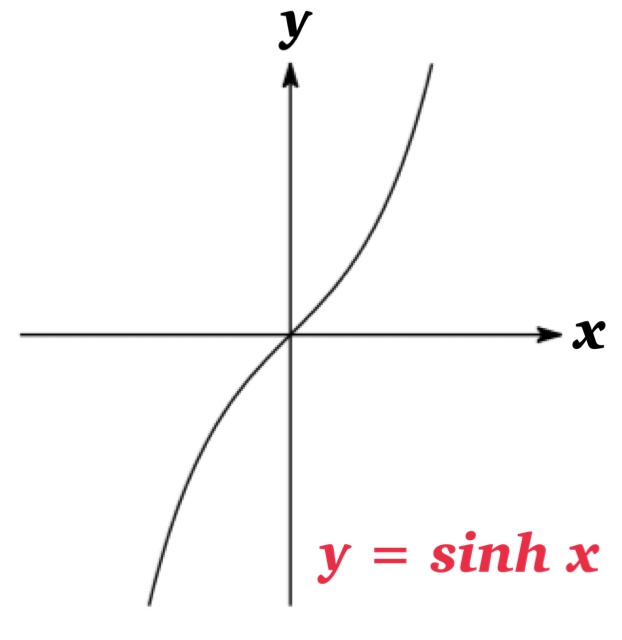
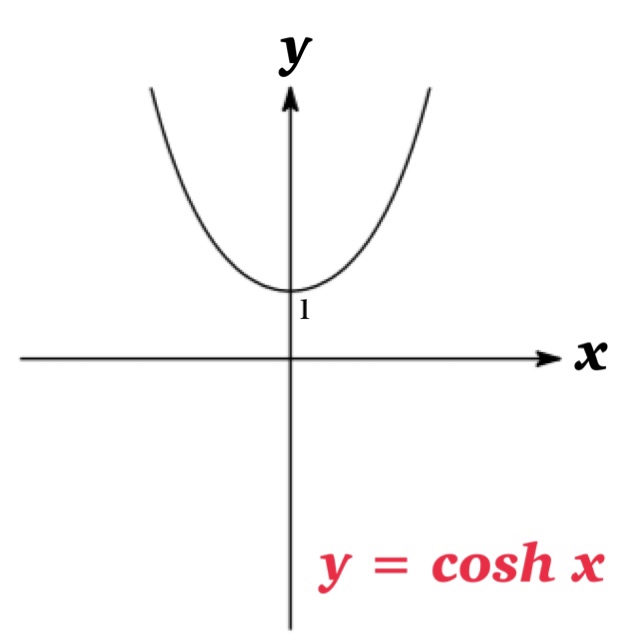
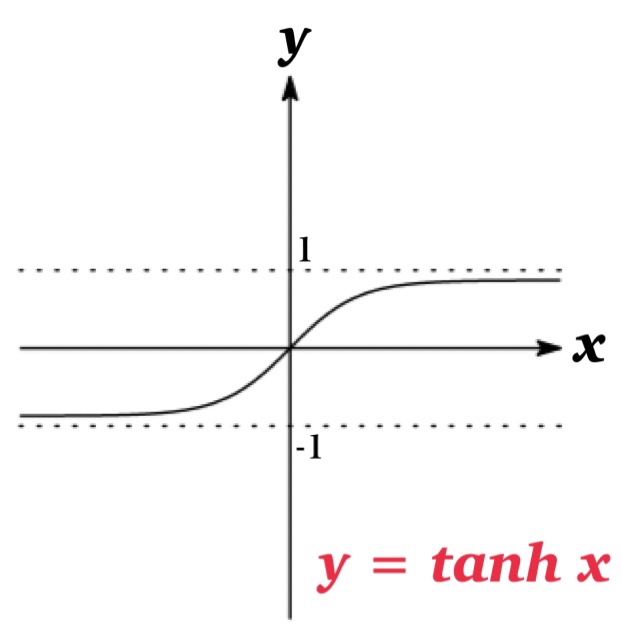
Hyperbolic Functions are analogous to the trigonometric functions, and have the same relationship to the hyperbola. Therefore they are collectively called hyperbolic functions and individually called hyperbolic sine, hyperbolic cosine and hyperbolic tangent.
Similar to the trigonometric identities, the others’ functions are also defined.
We also define \(\mathrm{csch} x, \mathrm{sech} x\) and \( \mathrm{coth} x\) as below:
$$\begin{eqnarray*}\mathrm{csch}\ x&=&\frac{1}{\sinh x} \\\mathrm{sech}\ x&=&\frac{1}{\cosh x} \\\mathrm{coth}\ x&=&\frac{1}{\tanh x}\end{eqnarray*}$$
Contents
Analogies to Trigonometric Functions
The hyperbolic functions satisfy identities similar to trigonometric identities.
Even Function ・ Odd Function
| Hyperbolic Functions | Trigonometric Functions | Even / Odd |
| \(\sinh (-x)=-\sinh x\) | \(\sin (-x)=-\sin x\) | Odd |
| \(\cosh (-x)=\cosh x\) | \(\cos (-x)=\cos x\) | Even |
| \(\tanh (-x)=-\tanh x\) | \(\tan (-x)=-\tan x\) | Odd |
Properties
| Hyperbolic Functions | Trigonometric Functions |
| \(\tanh x=\frac{\sinh x}{\cosh x}\) | \(\tan x=\frac{\sin x}{\cos x}\) |
| \(\cosh^{2} x-\sinh^{2} x=1\) | \(\sin^{2} x+\cos^{2} x=1\) |
| \(1-\tanh^{2} x=\frac{1}{\cosh^{2} x}\) | \(1+\tan^{2} x=\frac{1}{\cos^{2} x}\) |
The identity \(\cosh^{2} x-\sinh^{2} x=1\) gives the reason for the name “hyperbolic” functions. See also The Reason for the Name “Hyperbolic” Functions.
Addition Theorem
| Hyperbolic Functions | Trigonometric Functions |
| \(\sinh (x+ y)=\sinh x\cosh y+ \cosh x\sinh y\) | \(\sin (x+ y)=\sin x\cos y+ \cos x\sin y\) |
| \(\cosh (x + y)=\cosh x\cosh y+ \sinh x\sinh y\) | \(\cos (x + y)=\cos x\cos y- \sin x\sin y\) |
| \(\tanh (x + y)=\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}\) | \(\tan (x + y)=\frac{\tan x+\tan y}{1-\tan x\tan y}\) |
By substituting -y for y in above equations , we obtain the subtraction formulas \(\sinh (x- y), \cosh (x-y)\) and \(\tanh (x-y)\).
Example : \(\sinh \left(x+ (-y)\right)=\sinh x\cosh (-y)+ \cosh x\sinh (-y)=\sinh x\cosh y- \cosh x\sinh y\)
Derivatives
| Hyperbolic Functions | Trigonometric Functions |
| \((\sinh x)’=\cosh x\) | \((\sin x)’=\cos x\) |
| \((\cosh x)’=\sinh x\) | \((\cos x)’=-\sin x\) |
| \((\tanh x)’=\frac{1}{\cosh^{2} x} \) | \((\tan x)’=\frac{1}{\cos^{2} x}\) |
| \((\mathrm{csch}\ x)’=-\mathrm{csch}\ x \cdot\mathrm{coth}\ x\) | \((\mathrm{csc}\ x)’=-\mathrm{csc}\ x \cdot\mathrm{cot}\ x\) |
| \((\mathrm{sech}\ x)’=-\mathrm{sech}\ x \cdot\mathrm{tanh}\ x\) | \((\mathrm{sec}\ x)’=\mathrm{sec}\ x \cdot\mathrm{tan}\ x\) |
| \((\mathrm{coth}\ x)’=-\mathrm{csch}^{2}\ x\) | \((\mathrm{cot}\ x)’=-\mathrm{csc}^{2}\ x\) |
Integrals
By the derivatives formula, we have integration formulas as below:
| Hyperbolic Functions | Trigonometric Functions |
| \(\int \sinh x\ dx=\cosh x +C\) | \(\int \sin x\ dx=-\cos x +C\) |
| \(\int \cosh x\ dx=\sinh x +C\) | \(\int \cos x\ dx=\sin x +C\) |
| \(\int \tanh x\ dx=\ln \cosh x +C\) | \(\int \tan x\ dx=\ln |\sec x| +C\) |
| \(\int \mathrm{csch}\ x\ dx=\ln |\tanh \frac{x}{2}|+C\) | \(\int \csc x\ dx=\ln |\csc x-\cot x|+C\) |
| \(\int \mathrm{sech}\ x\ dx=\tan^{-1}|\sinh x|+C\) | \(\int \sec x\ dx=\ln |\sec x+\tan x|+C\) |
| \(\int \coth x\ dx=\ln |\sinh x|+C\) | \(\int \cot x\ dx=\ln |\sin x|+C\) |
Relationship between Hyperbolic and Trigonometric
We can express the trigonometric functions in terms of their hyperbolic functions as below: $$\sin x=-i\sinh ix\ \ \ \ \ \cos x=\cosh ix$$
These equations are derived by using Euler’s formula : \(\mathrm{e}^{ix}=\cos x+i\sin x\).
By substituting -x for x in Euler’s formula, we obtain \(\mathrm{e}^{-ix}=\cos x-i\sin x \ \ \ (*)\). From Euler’s formula and \((*)\), we get
$$\sin x=\frac{\rm{e}^{ix}-\rm{e}^{-ix}}{2i}\ \ \ \ \ \cos x=\frac{\rm{e}^{ix}+\rm{e}^{-ix}}{2}$$
From these relational expressions, it is natural that trigonometric functions and hyperbolic functions have similar properties. There are some differences in sign, but the differences are due to the imaginary unit “i”.
Related Articles
- Trigonometric Functions
- Inverse Hyperbolic Functions